Плоскость и тела

Легко представить себе поверхность как границу тела: плоская поверхность стола, сферическая поверхность мяча, цилиндрическая поверхность трубы. Но такое представление не полно. Возьмем тонкую замкнутую проволоку изогнутой формы и опустим её в мыльную пену. Если мы осторожно извлечем её из пены, то увидим, что просвет в проволочном "кольце" затянут тончайшей мыльной пленкой. Правильно представлять себе поверхность именно как тонкую пленку (но лишенную всякой толщины). Важнейшая и простейшая поверхность - плоскость. 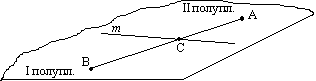Прямая m, лежащая в плоскости, разбывает её на две части - полуплоскости (см. рисунок); точки этой прямой и только они являются общими точками обеих полуплоскостей. Если А - точка одной полуплоскости, а В - другой, то отрезок АВ пересекает границу m полуплоскостей в некоторой точке С, лежащеймежду А и В. Плоскости задаются тремя точками и обозначаются часто так: плоскость АВС или PQR и т.д. Иногда бывает проще обозначать плоскость обной буквой греческого алфавита: a, b, g, d... Под фигурой обычно понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей). Под телом понимают обычно часть пространства, ограниченную какой-либо замкнутой поверхностью. Так, конус - тело, ограниченное канонической поверхностью с боков и плоским круглым основанием снизу. Куб - тело, ограниченное шестью квадратными гранями, и т.д. Курс геометрии традиционно подразделяется на планиметрию и стереометрию; в планиметрии рассматриваются свойства различных фигур (треугольников, многоугольников, окружностей), лежащих в плоскости. В стереометрии изучаются свойства пространственных фигур и тел.