Две прямые в пространстве могут быть расположены различным образом. Прежде всего, может случиться, что две прямые имеют общую точку, т.е. являются пересекающимися. Тогда они заведомо лежа в одной плоскости (аксиома 3). Возникла потребность рассмотреть следующую теорему
Теорема 1. В пространстве через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.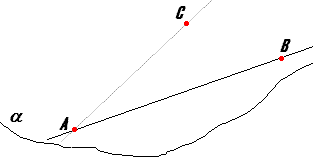
Доказательство: пусть АВ - данная прямая и С - не лежащая на ней точка. Проведем через точки А и С прямую (аксиома 1). Прямые АВ и АС различны, так как точка С не лежит на прямой АВ. Проведем через прямые АВ и АС плоскость α (аксиома 3). Она проходит через прямую АВ и точку С. Докажем, что плоскость α, проходящая через прямую АВ и точку С, единственна. Допустим, существует другая плоскость α', проходящая через прямую АВ и точку С. По аксиоме 2 плоскости α и α' пересекаются по прямой. Эта прямая должна содержать точки А, В и С. Но они не лежат на одной прямой. Мы пришли к противоречию. Теорема доказана.
Теорема 1.1. Через три точки, нележащие на одной прямой, всегда можно провести плоскость (и притом только одну).
Эта теорема доказывается очень просто. Достаточно провести через две из данных трех точек прямую и воспользоваться теоремой 1.
Напомним основные свойства плоскости.
Теорема 2. Прямая, две точки которой лежат в плоскости, вся лежит в этой плоскости (т.е. все её точки лежат в плоскости). Следовательно, если прямая не лежит в плоскости, то на не может иметь с ней более одной общей точки (точка пересечения прямой и плоскости).

Рассмотрим теперь случай, когда прямые не имеют общих точек. Это еще не означает, что они параллельны, т.к. определение параллельности предусматривает, что прямые принадлежат одной плоскости. Чтобы решить вопрос о расположении наших прямых, проведем через одну из них и произвольно взятую точку на другой прямой плоскость α. Возможны два случая: 1. Построенная плоскость содержит всю вторую прямую. В этом случае обе прямые принадлежат одной плоскости и не пересекаются и потому параллельны. Здесь нужно заметить пару утверждений. Предже всего, в пространстве как и на плоскости работает аксиома 9: через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. Из выше представленных рассуждений можно вывести следующую теорему:
Теорема 3. Параллельные прямые определяют плоскость и притом только одну.
Также в стереометрии (как и в планиметрии) работает следующая теорема:
Теорема 4. Если две прямые параллельны третей прямой, то они параллельны между собой.
Теорема 5. Два угла с соответственно параллельными и одинаково направленными сторонами равны.
2. Плоскость α пересекает прямую в точке А. Тогда обе прямые не лежат в одной плоскости. Такие прямые называют скрещивающимися.