| Главная Онлайн-расчеты Научный калькулятор | ||
ПризмаОпределение 1. Призматическая поверхностьТеорема 1. О параллельных сечениях призматической поверхности Определение 2. Перпендикулярное сечение призматической поверхности Определение 3. Призма Определение 4. Высота призмы Определение 5. Прямая призма Теорема 2. Площадь боковой поверхности призмы Параллелепипед: Определение 6. Параллелепипед Теорема 3. О пересечении диагоналях параллелепипеда Определение 7. Прямой параллелепипед Определение 8. Прямоугольный параллелепипед Определение 9. Измерения параллелепипеда Определение 10. Куб Определение 11. Ромбоэдр Теорема 4. О диагоналях прямоугольного параллелепипеда Теорема 5. Объем призмы Теорема 6. Объем прямой призмы Теорема 7. Объем прямоугольного параллелепипеда 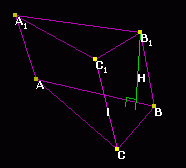 Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой.
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой.Грани, отличные от оснований, называются боковыми. Стороны боковых граней и оснований называются ребрами призмы, концы ребер называются вершинами призмы. Боковыми ребрами называются ребра, не принадлежащие основаниям. Объединение боковых граней называется боковой поверхностью призмы, а объединение всех граней называется полной поверхностью призмы. Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего основания или длина этого перпендикуляра. 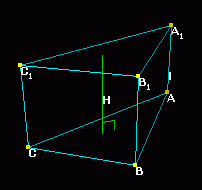 Прямой призмой называется призма, у которой боковые ребра перпендикулярны плоскостям оснований.
Прямой призмой называется призма, у которой боковые ребра перпендикулярны плоскостям оснований.
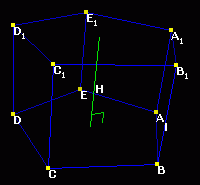 Правильной называется прямая призма (Рис.3), в основании которой лежит правильный многоугольник.
Правильной называется прямая призма (Рис.3), в основании которой лежит правильный многоугольник.
Обозначения: l - боковое ребро; P - периметр основания; So - площадь основания; H - высота; P^ - периметр перпендикулярного сечения; Sб - площадь боковой поверхности; V - объем; Sп - площадь полной поверхности призмы.
*При этом предполагается, что каждые две последовательные плоскости пересекаются и что последняя плоскость пересекает первую 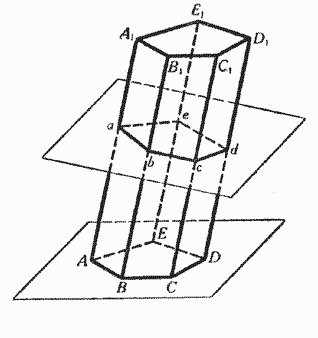
Теорема 1. Сечения призматической поверхности плоскостями, параллельными между собой (но не параллельными её рёбрам), представляют собой равные многоугольники. Пусть ABCDE и A'B'C'D'E' - сечения призматической поверхности двумя параллельными плоскостями. Чтобы убедиться, что эти два многоугольника равны, достаточно показать, что треугольники ABC и А'В'С' равны и имеют одинаковое направление вращения и что то же имеет место и для треугольников ABD и A'B'D', ABE и А'В'Е'. Но соответственные стороны этих треугольников параллельны (например АС параллельно А'С') как линии пересечения некоторой плоскости с двумя параллельными плоскостями; отсюда следует, что эти стороны равны (например АС равно А'С') как противоположные стороны параллелограмма и что углы, образованные этими сторонами, равны и имеют одинаковое направление. Определение 2. Перпендикулярным сечением призматической поверхности называется сечение этой поверхности плоскостью, перпендикулярной к её рёбрам. На основании предыдущей теоремы все перпендикулярные сечения одной и той же призматической поверхности будут равными многоугольниками. Определение 3. Призмой называется многогранник, ограниченный призматической поверхностью и двумя плоскостями, параллельными между собой (но непараллельными рёбрам призматической поверхности) Грани, лежащие в этих последних плоскостях, называются основаниями призмы; грани, принадлежащие призматической поверхности, - боковыми гранями; рёбра призматической поверхности - боковыми рёбрами призмы. В силу предыдущей теоремы, основания призмы - равные многоугольники. Все боковые грани призмы - параллелограммы; все боковые рёбра равны между собой. Очевидно, что если дано основание призмы ABCDE и одно из рёбер АА' по величине и по направлению, то можно построить призму, проводя рёбра ВВ', СС', .., равные и параллельные ребру АА'. Определение 4. Высотой призмы называется расстояние между плоскостями её оснований (НH'). Определение 5. Призма называется прямой, если её основаниями служат перпендикулярные сечения призматической поверхности. В этом случае высотой призмы служит, конечно, её боковое ребро; боковые грани будут прямоугольниками. Призмы можно классифицировать по числу боковых граней, равному числу сторон многоугольника, служащего её основанием. Таким образом, призмы могут быть треугольные, четырёхугольные, пятиугольные и т.д. Теорема 2. Площадь боковой поверхности призмы равна произведению бокового ребра на периметр перпендикулярного сечения. Пусть ABCDEA'B'C'D'E' - данная призма и abcde - её перпендикулярное сечение, так что отрезки ab, bc, .. перпендикулярны к её боковым ребрам. Грань АВА'В' является параллелограммом; его площадь равна произведению основания АА' на высоту, которая совпадает с аb; площадь грани ВСВ'С' равна произведению основания ВВ' на высоту bc и т. д. Следовательно, боковая поверхность (т. е. сумма площадей боковых граней) равна произведению бокового ребра, иначе говоря, общей длины отрезков АА', ВВ', .., на сумму ab+bc+cd+de+еа. |
||