Конус

Определения:
Определение 1. Конус
Определение 2. Круговой конус
Определение 3. Высота конуса
Определение 4. Прямой конус
Определение 5. Прямой круговой конус
Теорема 1. Образующие конуса
   Теорема 1.1. Осевое сечение конуса

Объем и площади:
Теорема 2. Объем конуса
Теорема 3. Площадь боковой поверхности конуса

Усеченный конус:
Теорема 4. Сечение, параллельное основанию
Определение 6. Усеченный конус
Теорема 5. Объем усеченного конуса
Теорема 6. Площадь боковой поверхности усеченного конуса

Определние
Тело ограниченное с боков конической поверхностью, взятой между её вершиной и плоскостью направляющей, и плоским основанием направляющей, образованным замкнутой кривой, называется конусом.


Основные понятия
Круговым конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.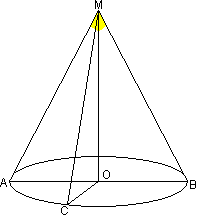

Прямым конусом называется конус, высота которого основанием содержит центр основания конуса.

Рассмотрим какую-либо линию (кривую, ломаную или смешанную)(например, l), лежащую в некоторой плокости, и произвольную точку ( например, М), не лежащую в этой плоскости. Всевозможные прямые, соединяющие точку М со всеми точками данной линии l, образуют поверхность, называемую канонической. Точка М является вершиной такой поверхности, а заданная линия l - направляющей. Все прямые соединяющие точку М со всеми точками линии l, называют образующими. Каноническая поверхность не ограничивается ни её вершиной, ни направляющей. Она простирается неограниченно в обе стороны от вершины. Пусть теперь направляющая - замкнутая выпуклая линия. Если направляющая - ломаная линия, то тело, ограниченное с боков канонической поверхностью, взятой между её вершиной и плокостью направляющей, и плоским основанием в плоскости направляющей, называется пирамидой.
Если же направляющая - кривая или смешанная линия, то тело, ограниченное с боков канонической поверхностью, взятой между её вершиной и плокостью направляющей, и плоским основанием в плоскости направляющей, называется конусом или
Определение 1. Конусом называют тело, состоящее из основания - плоской фигуры, ограниченной замкнутой линией (кривой или смешанной), вершины - точки, не лежащей в плокости основания, и всех отрезков, соединяющих вершину со всевозможными точками основания.
Все прямые, проходящие через вершину конуса и любую из точек кривой, ограничивающей фигуру основания конуса, называются образующими конуса. Чаще всего в геометрических задачах под образующей прямой имеется ввиду отрезок этой прямой, заключенный между вершиной и плоскостью основания конуса.
Основание ограниченной смешанной линией - это очень редкий случай. Он сдесь указан только потому, что он может быть рассмотрен в геометрии. Чаще рассматривается случай с криволинейной направляющей. Хотя, что случай с произвольной кривой, что случай со смешанной направляющей, мало чем полезен и в них сложно вывести какие-любо закономерности. Из числа конусов в курсе элементарной геометрии изучается прямой круговой конус.

Известно, что окружность есть частный случай замкнутой кривой линии. Круг - плоская фигура, ограниченная окружностью. Принимая окружность за направляющую, можно определеить круговой конус.
Определение 2. Круговым конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.
Определение 3. Высота конуса - перпендикуляр, опущенный из вершины на плокость основания конуса. Можно выделить конус, высота которого падает в центр плоской фигуры основания.
Определение 4. Прямым конусом называется конус, высота которого основанием содержит центр основания конуса.
Если связать эти два определения, мы получим конус, основание котрого есть круг, а высота падает в центр этого круга.
Определение 5. Прямым круговым конусом называют конус, основание котрого есть круг, а высота его соединяет вершину и центр основания данного конуса. Такой конус получается вращением прямоугольного треугольника вокруг одного из катетов. Поэтому прямой круговой конус является телом вращения и называется также конусом вращения. Если не оговорено противное, то для краткости в дальнейшем говорим просто конус.
Итак приведем некоторые свойства конуса:
Теорема 1. Все образующие конуса равны. Доказательство. Высота МО перпендикулярна всем прямым основания по определению перпендикулярной прямой к плокости. Поэтому треугольники МОА, МОВ и МОС являются прямоугольными и равны по двум катетам (МО - общая, ОА=ОВ=ОС - радиусы основания. Поэтому равны и гипотенузы, т.е. образующие.
Радиус основания конуса иногда называют радиусом конуса. Высота конуса называется также осью конуса, поэтому любое сечение, проходящее через высоту называется осевым сечением. Любое осевое сечение пересекает основание по диаметру (т.к. прямая, по которой пересекаются осевое сечение и плокость основания, проходит через центр окружности) и образует равнобедренный треугольник.
Теорема 1.1. Осевое сечение конуса есть равнобедренный треугольник. Так треугольник АМВ является равнобедренным, т.к. две его стороны МВ и МА есть образующие. Угол АМВ является углом при вершине осевого сечения.