| Главная Онлайн-расчеты Научный калькулятор | |
ПараллелограммОпределение 14. Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых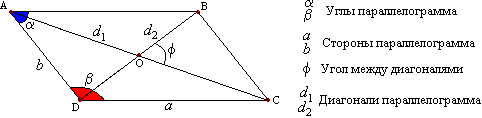 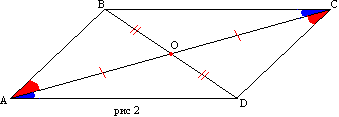 Теорема 22. Противоположные стороны параллелограма равны.
Теорема 22. Противоположные стороны параллелограма равны.Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠САВ=∠АСD, ∠АСВ=∠DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников: Теорема 23. Противоположные углы параллелограмма равны: ∠А=∠С и ∠В=∠D. Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD. Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов. Это так, потому что они являются внутренними односторонними углами. Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам. Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ОАD=∠ОСВ и ∠ОDА=∠ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д. Признаки параллелограмма Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом. Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ. Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом. Пусть ∠А=∠С и ∠В=∠D. Т.к. ∠А+∠В+∠С+∠D=360о, то ∠А+∠В=180о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению. Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом. Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению. Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм. Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1. Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом. Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4. В геометрии рассматривают частные случаи параллелограмма: прямоугольник, ромб, квадрат. Теорема 31. Площадь параллелограмма равна произведению стоны и проведенную к ней высоту.  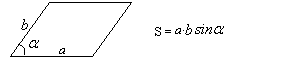 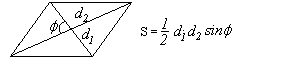 Теорема d2. (о сумме квадратов диагоналей параллелограмма): Сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон. Доказательство: Пусть ABCD - данный параллелограмм. Тогда: AB2 + BC2 + CD2 + AD2 = 2(AB2 + BC2) = = 2(AO2 + BO2 - 2AO·BO·cosAOB + + BO2 + CO2 - 2BO·CO·cosBOC) = = 2(2·(AO2 + BO2 - AO·BO(cosAOB - cosAOB))) = = 4(AO2+ BO2) = (2·AO)2 + (2·BO)2 = AC2 + BD2. Что и требовалось доказать. |
|