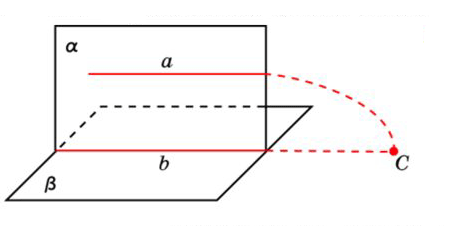
Определение 1. Прямая и плоскость называются параллельными, если они не пересекаются.
Теорема 1. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Доказательство. Пусть α - плоскость, а - не лежащая в ней прямая и b - прямая в плоскости α, параллельная прямой а. Проведем плоскость β через прямые а и b. Плоскость α и β пересекаются по прямой b. Если бы прямая а пересекала плоскость α, то точка пересечения принадлежала бы прямой b. Но это невозможно, т.к. прямые а и b параллельны. Итак, прямая а не пересекает плоскость α, а значит, параллельна ей. Теорема доказана.