Параллельные и перпендикулярные прямые

Определение.1. Параллельные прямое
Определение.2. Перпендикулярные прямые
Теорема.1. I свойство параллельных прямых
Теорема.2. II свойство параллельных прямых
Теорема.3. III свойство параллельных прямых
Теорема.4. IV свойство параллельных прямых
Теорема.5. V свойство параллельных прямых
Теорема.6. I признак параллельных прямых
Теорема.7. II признак параллельных прямых
Теорема.8. III признак параллельных прямых
Теорема.9. IV признак параллельных прямых
Теорема 10. V признак параллельных прямых
Теорема 11. Две прямые, параллельные третей
   Теорема 11.1 Следствие
Теорема 12. Прямая, пересекающая одну из параллельных прямых
Теорема 13. Отрезки параллельных прямых
Теорема 14. Теорема Фалеса
   Теорема 14.1. Параллельные прямые, пересекающие стороны угла
Теорема 15. Прямая, перпендикулярна одной из параллельных прямых
Теорема 16. Две (и более) прямые, перпендикулярные третей прямой

Определение 1. Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали.
На рисунке a и b. 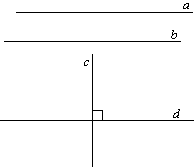Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.
На рисунке c и d.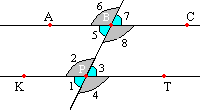
При пересечении пары прямых (параллельных в данном случае) некой прямой (такая прямая называется секущей прямой) образуются (акромя пройденных нами в теме углы смежных и вертикальных) следующие углы:
Внутренние накрестлежащие углы - 2 и 8; 3 и 5
Внешние накрестлежащие углы - 1 и 7; 4 и 6
Внутренние односторонние углы - 2 и 5; 3 и 8
Внешние односторонние углы - 1 и 6; 4 и 7
Соответственные углы - 1 и 5; 2 и 6; 3 и 7; 4 и 8
Между этими углами можно вывести закономерности. Свойства параллельных прямых:
Теорема 1. Внутренние накрестлежащие углы равны

Доказательство: Пусть a и b - две параллельные прямые, c - секущая, A и B - точки пересечения секущей с этими прямыми. Пусть утверждение теоремы ложно. Проведем тогда через точку A прямую d, такую что внутренние накрест лежащие углы при прямых b и d и секущей c равны. Тогда по первому признаку параллельности прямых, прямые b и d параллельны. Но прямые b и a параллельны. Значит, через точку A проходят две прямые - a и d, параллельные прямой b. Это противоречит IX аксиоме. Значит, утверждение теоремы верно. Теорема доказана.
Теорема 2. Внешние накрестлежащие углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 3. Сумма внутренних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 4. Сумма внешних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 5. Соответственные углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.

Признаки параллельных прямых: 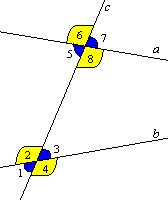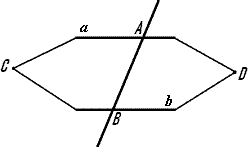Теорема 6. Если при пересечении двух прямых а и b третей прямой с внутренние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Пусть прямые a и b пересекаются секущей в точках A и B, но прямые a и b пересекаются в точке C (рис. 15). Секущая c разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник ABD, равный треугольнику ABC, с вершиной D в другой полуплоскости. Угол DAB равен углу ABC, а значит, точка D лежит на прямой a по условию. Аналогично точка D лежит на прямой b. Следовательно, точка D принадлежит прямым a и b. Значит, прямые a и b пересекаются в двух точках - C и D. Противоречие. Значит, исходное предположение не верно. Теорема доказана.
Теорема 7. Если при пересечении двух прямых а и b третей прямой с внешние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 8. Если при пересечении двух прямых а и b третей прямой с сумма внутренних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 9. Если при пересечении двух прямых а и b третей прямой с сумма внешних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 10. Если при пересечении двух прямых а и b третей прямой с соответственные углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.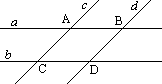
Теорема 11. Две прямые, параллельные третей, параллельны.

Доказательство: Пусть прямые a и b параллельны прямой c. Допустим, что прямые a и b не па-раллельны. Тогда либо прямые a и b совпадают, что противоречит условию, либо пересекаются в не-которой точке S. Тогда через точку S проходит две прямые - a и b, параллельные прямой c, что противоречит IX аксиоме. Значит, исходное предположение не верно. Теорема доказана.
Теорема 11.1. Если параллельно одной из двух параллельных прямых провести третью прямую, вторая из этих прямых либо параллельна третьей, либо совпадает с ней.

Доказательство: Очевидно из теоремы 11 параллельности прямых.
Теорема 12. Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Теорема 13. Отрезки параллельных прямых, заключенные между некой (иной) парой параллельных прямых, равны.
Теорема 14. (Теорема Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.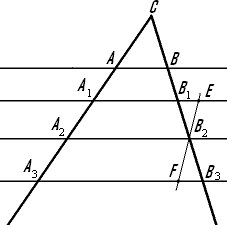

Доказательство: Пусть A₁, A₂, A₃ - точки пересечения параллельных прямых с одной из сторон угла, и точка A₂ лежит между точками A₁ и A₃. Пусть B₁, B₂, B₃ - соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A₁A₂ = A₂A₃, то B₁B₂ = B₂B₃. Проведем через точку B₂ прямую EF, параллельную прямой A₁A₃. Треугольники EB₂B₁ и FB₂B₃ равны по второму признаку равенства треугольников. У них стороны EB₂ и FA₂ равны по условию, углы B₁B₂E и B₃B₂F равны как вертикальные, а углы B₁EB₂ и B₂FB₃ равны как внутренние накрест лежащие при секущей EF. Значит, B₁B₂ = B₂B₃. Что и требовалось доказать.
Теорема 14.1.. Параллельные прямые, пересекая стороны угла, отсекают пропорциональные отрезки.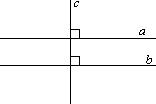

Теорема 15. Две (и более) прямые, перпендикулярные третей прямой, параллельны.

Доказательство: Действительно, внутренние накрест лежащие углы равны 90°. Следовательно, по первому признаку параллельных прямых, эти прямые параллельны.
Теорема 16. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.

Доказательство: Очевидно из теоремы 15.