Определение 1. Пирамидой называется тело, образованное плоским многоугольником (основание), точкой, нележащей в плоскости этого многоугольника (вершина), и всех отрезков, соединяющих точки основания с вершиной.
Определение 2. Стороны основания есть ребра основания.
Определение 3. Прямые, соединяющие вершины основания с вершиной трапеции, есть боковые ребра.
Определение 4. Совокупности прямых, соединяющих каждую по отдельности сторону основания с вершиной, называются боковыми гранями.
Определение 5. Совокупность боковых граней задает боковую поверхность пирамиды.
Определение 6. Высота, проведенная в боковой грани из вершины пирамиды на сторону основания, называется апофемой.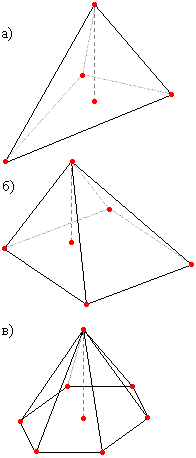
Пирамиды классифицируются по числу сторон многоугольника, лежащего в их основании. Говорят о треугольной , четырехугольной и вообще n-угольной пирамидах. Чаще всего в задачах встречаются треугольные (рис. а), четырехугольные (рис. б) и (совсем редко) шестиугольные (рис. в).

Заметим, что n-угольная пирамида имеет n+1 граней: n боковых граней и основание. При вершине пирамиды мы имеем n-гранный угол с n плоскими и n двугранными углами. Они соответственно называются плоскими углами при вершине и двугранными углами при боковых ребрах. Итак заключаем:
Определение 7. Углы при вершине боковых граней называются плоскими углами при вершине пирамиды.
Определение 8. Двугранные углы, образованные смежными боковым гранями, называются двугранными углами при боковых ребрах пирамиды.
При вершинах основания мы имеем n трехгранных углов. Здесь:
Определение 9.Плоские углы, образованные боковыми ребрами и сторонами основания, называются плоскими углами при основании.
Определение 10.Двугранные углы между боковыми гранями и плоскостью основания называются двугранными углами при основании.
Определение 11.Треугольная пирамида иначе называется тетраэдром (т.е. четырехгранником). Особенность тетраэдра в том, что любая из его граней может быть принята за основание.