Определение 12. Пирамида называется правильной, если в её основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).
Заметим, что правильная пирамида не является, вообще говоря, правильным многогранником.
Отметим некоторые свойства правильной n-угольной пирамиды на примере треугольной пирамиды. Как известно центр правильного треугольника (пересечение медиан) совпадает с центром вписанной (пересечение биссектрис) и описанной около него окружности (пересечение серединных перпендикуляров). Т.е. отрезки АО, ВО и СО являются радиусами описанной окружности и равны.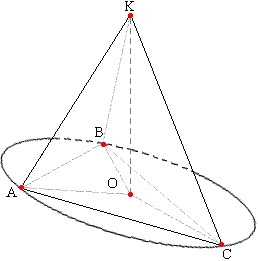
Поэтому прямоугольные треугольники АОМ, ВОМ и СОМ равны по двум катетам (МО-общая). Из равенства этих треугольников следует равенство соответствующих сторон: АМ=ВМ=СМ
Теорема 1. В правильной n-угольной пирамиде все боковые ребра равны между собой.
Из равенства ребер следует и равенство боковых граней. Треугольники АВМ, ВСМ и АСМ равны по трем сторонам.
Теорема 2. Все боковые грани правильной n-угольной пирамиды суть равные равнобедренные треугольники (углы при основании рабнобедренного треугольника равны), поэтому:
Теорема 2.1. В правильной n-угольной пирамиде все плоские углы при вершине равны;
Теорема 2.2. В правильной n-угольной пирамиде все плоские углы при основании равны.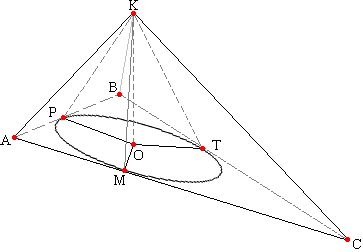
Как известно радиусы перпендикулярны касательной в точке касания. Проведем радиусы вписанной окружности ОТ, ОР и ОМ. Соединим соответственной точки Т, Р и М с вершиной К. Прямые КТ, КР и КМ соответственно перпендикулярны сторонам основания ВС, АВ и АС по теореме о трех перпендикулярах. Из равенства прямоугольных треугольников ОРК, ОТК и ОКМ по двум катетам (ОТ=ОР=ОМ как радиусы вписанной окружности; МО - общая) следует равенство всех двугранных углов при основании пирамиды РОРМ=РОТМ=РОКМ
Теорема 3. В правильной n-угольной пирамиде все двугранные углы при основании равны.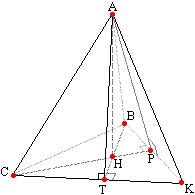
Теорема 4. В правильной n-угольной пирамиде все двугранные углы при боковых ребрах равны.