Вспомним: апофема-высота боковой грани пирамиды, проведенная из вершины на ребро основания.
Теорема 5. Если все боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга.
Эту теорему можно сформулировать и так:
Теорема 5.1. Если все апофемы пирамиды равны, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга.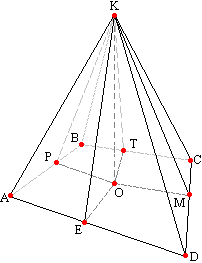
Докажем теорему на при мере четырехугольной пирамиды. Пусть дана пирамида КABCD, К -вершина, АВСD - основание. Проведем высоту КО пирамиды. В каждой боковой грани проведем высоту из вершины пирамиды на сторону основания. В плоскости основания соединим точку О (основание высоты) с точкой основаниями этих высот - апофем. ОР, ОТ, ОМ и ОЕ соответственно перпендикулярны АВ, ВС, CD и AD (теорема о трех перпендикулярах). По определению углы КРО, КТО, КМО, КЕО - линейные углы двугранных углов между соответственными боковыми гранями и основанием ABCD. Высота КО является перпендикуляром к основанию, поэтому перпендикулярна любой прямой в этой плоскости, т.е. перпендикулярна прямым ОР, ОТ, ОМ и ОЕ. Это говорит, что треугольники КРО, КТО, КМО, КЕО прямоугольные.
По условию (теорема 5) углы КРО, КТО, КМО, КЕО равны. Рассмотрим треугольники КРО, КТО, КМО, КЕО, они прямоугольны и равны (по катету и острому углу, КО - общая и углы КРО, КТО, КМО, КЕО равны по условию).
По условию (теорема 5.1) КР, КТ, КМ и КЕ равны, поэтому треугольники КРО, КТО, КМО, КЕО прямоугольные и равны по катету и гипотенузе.
Из равенства этих треугольников следует, что их соответствующие стороны ОР, ОТ, ОМ и ОЕ равны, а значит, в четырехугольнике ABCD есть такая точка, которая равноудалена от его сторон, то есть в него можно вписать круг.

Теорема 6. Если все боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.
Эту теорему можно сформулировать и так:
Теорема 6.1. Если все боковые ребра пирамиды равны, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.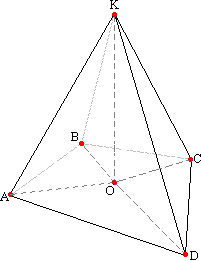
Докажем теорему на при мере четурехугольной пирамиды. Пусть дана пирамида КABCD, К -вершина, АВСD - основание. Проведем высоту КО пирамиды. В плоскости основания соединим точку О (основание высоты) со всеми вершинами основания А, В, С и D. Угол KВО - угол между ребром КB и плоскостью основания (угол между прямой и плоскостью есть угол между этой прямой и её проекцией на эту плоскость). Таким же образом докажем, что углы КСО, КАО и KDO - углы, образованные соответствующими ребрами КС, КА и KD с плоскостью основания. Высота КО является перпендикуляром к основанию, поэтому перпендикулярна любой прямой в этой плоскости, т.е. перпендикулярна прямым ОА, ОВ, ОС и ОD. Это говорит, что треугольники КAО, КBО, КCО, КDО прямоугольные.
Углы КВО, КСО, КАО и KDO равны (по условиям теоремы 6). Рассмотрим треугольники КAО, КBО, КCО, КDО, они прямоугольны и равны (по катету и острому углу, КО - общая и углы КАО, КВО, КСО, КDО равны по условию).
Доказывая теорему 6.1, также рассмотрим треугольники КAО, КBО, КCО, КDО, они прямоугольны и равны по катету и гипотенузе (КО - общая, КА=КВ=КС=KD по условию теоремы).
Из равенствa этих треугольников следует, что их соответствующие стороны ОА, ОВ, ОС и ОD равны, а значит, в основании есть такая точка, которая равноудалена от вершин четырехугольника ABCD, то есть около него можно описать окружность.