| Главная Онлайн-расчеты Научный калькулятор | |
|
Определение 18. Часть пирамиды, образованная при сечении пирамиды плоскостью, параллельной её основанию, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.
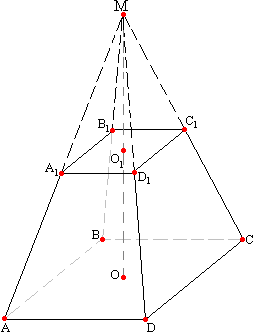 На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h2/h1, или боковых ребер, или других соответствующих линейных размеров обеих пирамид.
Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как
На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h2/h1, или боковых ребер, или других соответствующих линейных размеров обеих пирамид.
Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как
Объемы подобных тел относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований. Пусть дана усеченная пирамида с высотой h и площадями оснований S1 и S2. Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S2/S1. Высота усеченной пирамиды выражается как h = h1 - h2 = h1(1 - k). Теперь имеем для объема усеченной пирамиды (через V1 и V2 обозначены объемы полной и малой пирамид) 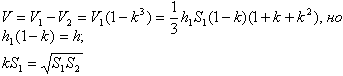 k2ЧS1=S2, поэтому Теорема 15. Объем усеченной пирамиды можно вычислить по формуле: Теорема 16. Если все апофемы усеченной пирамиды равны, то площадь её боковой поверхности можно вычислить по формуле: Теорема 16.1. Если все боковые грани усеченной пирамиды наклонены к плоскости основания под одинаковым углом, то площадь её боковой поверхности можно вычислить по формуле: Выведем эту формулу. Пусть S - площадь боковой поверхности усеченной пирамиды, обладающей одним из вышеперечисленных признаков, Р1 и Р2 - периметры оснований и а - длина апофемы. Рассуждаем точно так же, как и при выводе формулы для объема. Дополняем пирамиду верхней частью, имеем P2 = kP1, S2=k2S1, где k - коэффициент подобия, P1 и P2 - периметры оснований, а S1 и S2 - лощади боковых поверхностей всей полученной пирамиды и её верхней части соответственно. Для боковой поверхности найдем (а1 и а2 - апофемы пирамид, а = а1 - а2 = а1(1-k)): 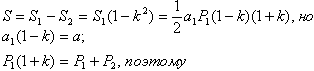 Правильная усеченная пирамида также как и обычная правильная пирамида имеет особенности: Теорема 17. В правильной усеченной n-угольной пирамиде все боковые ребра равны между собой. Теорема 18. Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях рабнобедренной трапеции равны), поэтому: Теорема 18.1. В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны. Теорема 19. В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны. Теорема 20. В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны. |
|