Определение 6. Параллелепипедом называется призма, основаниями которой служат параллелограммы. При этом все грани будут параллелограммами.
Каждый параллелепипед можно рассматривать как призму тремя различными способами, так как за основания можно принять каждые две противоположные грани (на черт. 5 грани ABCD и A'B'C'D', или АВА'В' и CDC'D', или ВСВ'С' и ADA'D').
Рассматриваемое тело имеет двенадцать рёбер, по четыре равных и параллельных между собой.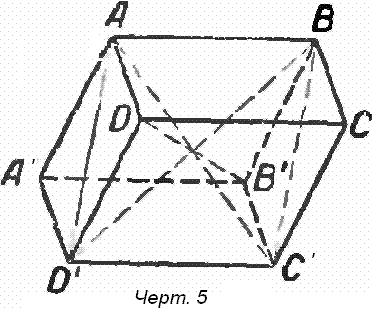
Теорема 3. Диагонали параллелепипеда пересекаются в одной точке, совпадающей с серединой каждой из них.
Параллелепипед ABCDA'B'C'D' (черт. 5) имеет четыре диагонали AC', BD', CA', DB'. Мы должны доказать, что середины двух каких-либо из них, например АС и BD', совпадают. Это следует из того, что фигура ABC'D', имеющая равные и параллельные стороны АВ и C'D', есть параллелограмм.
Определение 7. Прямым параллелепипедом называется параллелепипед, являющийся одновременно и прямой призмой, т. е. параллелепипед, боковые рёбра которого перпендикулярны к плоскости основания.
Определение 8. Прямоугольным параллелепипедом называется прямой параллелепипед, основанием которого служит прямоугольник. При этом все его грани будут прямоугольниками.
Прямоугольный параллелепипед представляет собой прямую призму, какую бы из его граней мы ни приняли за основание, так как каждое его ребро перпендикулярно к рёбрам, выходящим с ним из одной вершины, и будет, следовательно, перпендикулярно и к плоскостям граней, определяемых этими рёбрами. В противоположность этому прямой, но не прямоугольный, параллелепипед можно рассматривать как прямую призму только одним способом.
Определение 9. Длины трёх рёбер прямоугольного параллелепипеда, из которых никакие два не параллельны между собой (например трёх рёбер, выходящих из одной вершины), называются его измерениями. Два |прямоугольных параллелепипеда, имеющих соответственно равные изме- рения, очевидно, равны между собой.
Определение 10.Кубом называется прямоугольный параллелепипед, все три измерения которого равны между собой, так что все его грани - квадраты. Два куба, рёбра которых равны между собой, равны.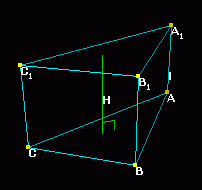
Определение 11. Наклонный параллелепипед, у которого все рёбра равны между собой и углы всех граней равны или пополнительны, называется ромбоэдром.
Все грани ромбоэдра - равные ромбы. (Форму ромбоэдра имеют некоторые кристаллы, имеющие большое значение, например кристаллы исландского шпата.) В ромбоэдре можно найти такую вершину (и даже две противололожные вершины), что все прилежащие к ней углы равны между собой.
Теорема 4. Диагонали прямоугольного параллелепипеда равны между собой. Квадрат диагонали равен сумме квадратов трёх измерений.
В прямоугольном параллелепипеде ABCDA'B'C'D' (черт. 6) диагонали АС' и BD' равны, так как четырёхугольник ABC'D' - прямоугольник (прямая АВ перпендикулярна к плоскости ВСВ'С', в которой лежит ВС').
Кроме того, AC'²=BD'² = AB2+AD'² на основании теоремы о квадрате гипотенузы. Но на основании той же теоремы AD'² = AA'²+ +A'D'²; отсюда имеем:
АС'² = АВ² + АА'²+A'D'²=АВ² + AA'² + AD².

Теорема 5. Объем призмы равен произведению площади его ортогонального сечения и высоты.

Теорема 6. Объем прямой призмы равен произведению высоты и площади его основания

Теорема 7. Объем прямоугольного параллелепипеда равен произведению его измерений.