Прямоугольник

Определение 15. Прямоугольник - это параллелограмм , у которого все углы прямые (равны 90 градусам). Как частный случай параллелограмма прямоугольник имеет все его свойства, но есть и частное. Рассмотрим его:
Теорема 34. Диагонали прямоугольника равны.
Для доказательства достаточно рассмотреть на рис1 два прямоугольных треугольника ADB и АВС. Они равны по двум катетам (противолежащие стороны равны), поэтому равны и их гипотенузы - диагонали АС и ВD.
Также прямоугольник имеет все признаки параллелограмма, но и тут есть частный признак:
Теорема 35. Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то такой четырехугольник является прямоугольником.
Из равенства диагоналей следует и равенство частей, на которые они разбиваются при пересечении. Т.е. точка пересечения диагоналей равноудалена от вершин четырехугольника, а следовательно около него можно описать окружность. Зная теорему: вписанные углы, опирающиеся на диаметр, равны 90 градусов, заключаем, что все углы данного четырехугольника прямые. Из этого доказательства также вытекает и следующее утверждение:
Теорема 36. Диаметр описанной около прямоугольника окружности равен его диагонали.
Площадь прямоугольника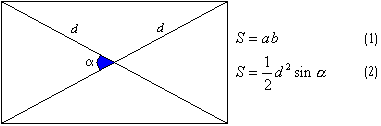
Первая формула считается стандартом и не нуждается в доказательстве, а вторая является следствием формулы площади четырехугольника с поправкой на то, что диагонали равны.



Теорема 37. Площадь прямоугольника равна половине произведения квадрата диагонали и синуса угла между диагоналями.