Многоугольник

Определение 1. Простая замкнутая ломаная называется многоугольником.
Вершины ломаной называются вершинами многоугольника, а звенья ломаной - сторонами многоугольника. Отрезки, соединяющие не соседние вершины ломаной, называются диагоналями.
Многоугольник с n вершинами, а значит и с n сторонами называется n-угольником. Плоским многоугольником или многоугольной областью называется часть плоскости, ограниченная многоугольником. При этом считается, что стороны многоугольника не принадлежат плоскому многоугольнику.
Определение 2. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
При этом сама прямая считается принадлежащей полуплоскости. Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.
Сумма длин всех сторон многоугольника составляет его периметр.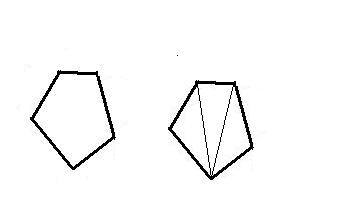
Теорема 1. Сумма углов выпуклого n-угольника равна
180°•(n - 2) градусов.

Доказательство: Многоугольников с n меньше трех не существует. При n = 3 многоугольник есть треугольник, и сумма его углов действительно равна 180°. Пусть n>3, A₁A₂A₃ … A_n - данный многоугольник. Проведем n - 3 диагонали: A₁A₃, A₁A₄, A₁A₅, …, A₁A_n-1 (рис. 1). Этот многоугольник выпуклый, а значит, эти диагонали разбивают его на n-2 треугольника: ?A₁A₂A₃, ?A₁A₃A₄, …, ?A₁A_n-1A_n. Сумма углов многоугольника совпадает с суммой углов этих треугольников. А сумма углов n - 2 треугольников есть 180°•(n - 2). Теорема доказана.

Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине.
Теорема 1.1. Сумма внешних углов многоугольника есть 360°.
Определение 3. Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Определение 4. Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
Определение 5. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.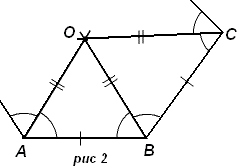

Теорема 2. Правильный выпуклый многоугольник является вписанным и описанным около окружности. Центр вписанной и описанной окружностей совпадают.

Доказательство: Пусть A, B и C - три соседние вершины правильного многоугольника (рис. 2). Проведем биссектрисы углов A и B. Пусть O - точка их пересечения. BO - биссектриса угла B, а значит угол ABO равен углу CBO. Также AB=BC, BO=BO. Следовательно, ∠ABO = ∠CBO, а значит AO=BO, BO=CO, то есть окружность с центром в точке O, проходящая через точки A и B, проходит через точку C.
Аналогично доказывается, что эта окружность проходит через остальные вершины многоугольника. Итак, O - центр окружности, описанной около многоугольника. Следовательно, точка O равноудалена от концов всех сторон этого многоугольника. Значит, точка O лежит всех серединных перпендикулярах, проведенных к сторонам данного многоугольника. Значит, все серединные перпендикуляры к сторонам многоугольника пересекаются в точке O. Так как треугольники AOB и BOC равны, расстояние от точки O до прямых AB и BC равны. Аналогично доказывается, что точка O равноудалена от других сторон данного многоугольника. Следовательно, O - центр окружности, вписанной в многоугольник. Значит, центры вписанной и описанной около данного многоугольника окружности, совпадают. Теорема доказана полностью.