Прямоугольный треугольник

Определение 2.1. Прямоугольным называется треугольник, у которого один из углов прямой.
Это значит, что прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы). Сумма двух острых углов прямоугольного треугольника равна прямому углу. Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника. Другая особенность прямоугольного треугольника состоит в
Теорема 24. Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.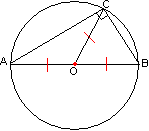
Данная окружность является описанной для данного треугольника АВС, а угол АСВ является вписанным в эту окружность. Из темы круг и окружность знаем, что вписанный в окружность прямой угол опирается на диаметр. Поэтому гипотенуза АВ является диаметром. Центр окружности - точка О - лежит в его середине. Отрезок ОС является радиусом, т.к. соединяет центр с точкой окружности, также является медианой треугольника АВС, т.к. соединяется его вершину С с серединой противоположной стороны АВ. Отсюда:
Теорема 24.1 Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.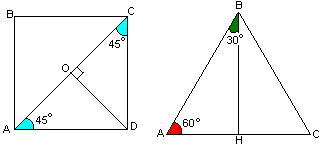

Отметим еще два специальных вида прямоугольных треугольников: равнобедренный и пр. тр. с углами в 30° и 60°. Равнобедренный прямоугольный треугольник имеет равные углы при основании (гипотенузе). Каждый из этих углов содержит 45°. Такой треугольник получается, если рассечь квадрат его диагональю. Высота равнобедренного прямоугольного треугольника, проведенная из вершины прямого угла, делит его на два равнобедренных прямоугольных треугольника.
Прямоугольный треугольник с углами в 30° и 60° получится, если в равностороннем треугольнике провести одну из его высот и взять какой-либо из двух равных прямоугольных треугольников, на которые она разбивает данный равносторонний треугольник. Обратно, если взять прямоугольный треугольник с углами в 30° и 60°, то, приложив к нему еще один такой же треугольник, имеющий с ним общий катет, прилежащий к углу в 30°, получим равносторонний треугольник. Из такого способа получения указанного треугольника видно, что в прямоугольном треугольнике с углами в 30° и 60° катет, лежащий против угла в 30°, равен половине гипотенузы.

Рассмотрим произвольный прямоугольный треугольник АВС (см. рис. 1) и проведем высоту СН = h из вершины С его прямого угла. Она разобьет данный треугольник на два прямоугольных треугольника АСН и ВСН; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС. Все три треугольника АВС, АСН и ВСН подобны между собой. Из подобия треугольников АВС и АСН имеем СН² = АН?ВН, т.е.
Теорема 25. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому отрезков, на которые она разбивает гипотенузу.
Далее, из подобия треугольников АВС и АСН найдем АС² = АН?ВА. Аналогичным образом найдем ВС² = АВ?ВН.
Теорема 26. Катет прямоугольного треугольника равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Запишем эти теоремы в виде формул для нашего треугольника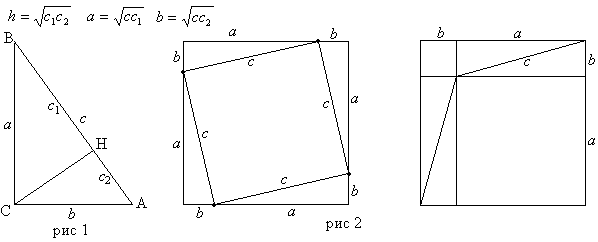

Теорема 27. Теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы:
a²+b²=c²

Доказательство: Запишем выражения квадратов катетов а и b треугольника:
a²=cc₁, b²=cc₂,
и сложим эти неравенства почленно. Получим
a²+b²= cc₁+cc₂= c(c₁+c₂)=c²,
что и требовалось доказать.
Приведенное доказательство имеет алгебраический характер: вычисление показывает, что сумма квадратов длин катетов равны квадрату длины гипотенузы. Поскольку квадрат длины отрезка геометрически можно истолковать как площадь квадрата, построенного на этом отрезке, как на стороне, то теорему Пифагора можно сформулировать в чисто геометрических терминах: сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе. В связи с этим на рисунке 2 дано геометрическое обоснование теоремы Пифагора. Один и тот же квадрат со стороной a+b разложен в одном случае на четыре равных прямоугольных треугольника с катетами а,b и квадрат со стороной с, а в другом случае – на такие же четыре равных прямоугольных треугольника и на два квадрата со сторонами а и b соответственно. Из этого непосредственно видно, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.

ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ:

1. По катету и гипотенузе;

2. По двум катетам;

3. По катету и острому углу;

4. По гипотенузе и острому углу.