Ромб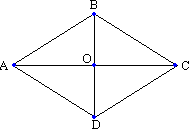

Определение 16. Ромб - это параллелограмм , у которого все стороны равны.
Как частный случай параллелограмма ромб имеет все его свойства, но есть и частные. Запишем их:
Теорема 38. Диагонали ромба перпендикулярны.
Для доказательства достаточно увидеть, что все четыре треугольника, на которые ромб разбивается диагоналями, равны по трем сторонам (стороны равны, диагонали точкой пересечения делятся пополам). Т.е. углы АОВ, ВОС, СОD, DОА равны, а в сумме они составляют 360 градусов, поэтому каждый из них по 90.
Теорема 39. Диагонали ромба являются биссектрисами его углов.
Для доказательства достаточно увидеть, что все четыре треугольника, на которые ромб разбивается диагоналями, равны по трем сторонам (стороны равны, диагонали точкой пересечения делятся пополам). Поэтому равны и соответственные углы. Например, ∠АВО=∠СВО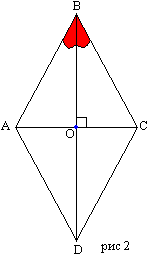

Признаки, с помощью которых можно доказать, что данный параллелограмм - ромб:
Теорема 40. Если в параллелограмме диагонали перпендикулярны, то он - ромб.
Для доказательства достаточно увидеть, что все четыре треугольника, на которые ромб разбивается диагоналями, прямоугольные и равны по двум катетам (диагонали ромба точкой пересечения делятся пополам). Поэтому равны и их гипотенузы, т.е. все стороны параллелограмма равны между собой.
Теорема 41. Если в параллелограмме диагонали являются биссектрисами его углов, то он - ромб.
Для доказательства достаточно увидеть, что все четыре треугольника, на которые ромб разбивается диагоналями, равны по стороне и двум углам (противоположные углы ромба равны, значит и их половины равны). Для треугольников АВО и СВО - ВО - общая, углы АВО и СВО равны и ВАО и ВСО равны (как половины противоположных углов). Поэтому равны и их соответственные стороны, т.е. все стороны параллелограмма равны между собой.

Признаки, с помощью которых можно доказать, что данный четырехугольник - ромб можно вывести сложив 5 признаков из темы параллелограмм и 2 признака из этой темы. Всего получится 10 признаков. Но легче доказать сначала, что четырехугольник - параллелограмм, а затем доказать, что он - робм, используя эти признаки.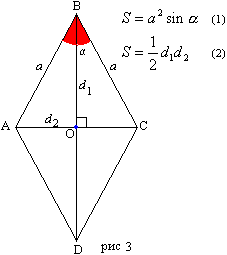
Первая формула является следствием формулы площади параллелограмма (с учетом равенства сторон), а вторая - следствием формулы площади четырехугольника (с учетом угла между диагоналями).
Теорема 42. Площадь ромба равна произведению квадрата его стороны и синуса острого угла.
Теорема 43. Площадь ромба равна половине произведения диагоналей.