Задача №1

Даны две вершины треугольника М ₁ (-10;2) и М₂ (6;4); его высоты пересекаются в точке Н (5;2). Определить координаты третьей вершины М₃.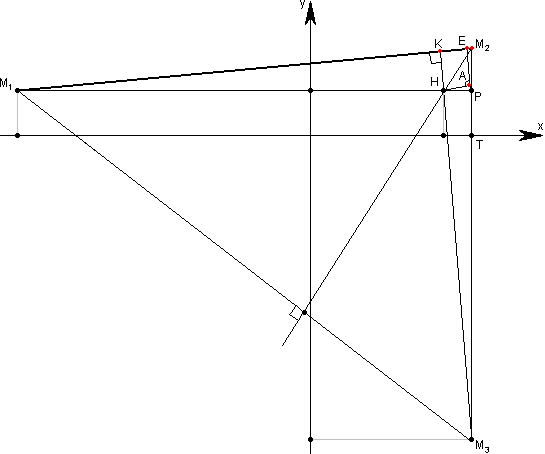

Разметим соответствующие точки.
Прямая М₁Н принадлежит высоте треугольника опущенной из вершины М₁.
Точки М₁ и Н имеют одинаковую координату у значит прямая М₁Н параллельна оси х, а значит и высота, частью которой она является, тоже параллельна оси х, а значит все прямые ей перпендикулярные – параллельны оси у. Из точки М₂ проведем прямую параллельно оси у. На этой прямой лежит вся сторона М₂М₃ то есть и точка М₃ тоже. Т.к. эта прямая параллельна оси у, то координаты х всех точек лежащих на этой прямой одинакова и равна 6 (т.к. у точки М₂ так)
Координатой у точки М₃ является расстояние ТМ₃.
Рассмотрим треугольник М₁М₂Т
В нем М₁Т = 16, а М₂Т = 2(по координатам точек)


Теперь из точки Р на сторону М₁М₂ опустим перпендикуляр РЕ

Теперь из точки Н опустим перпендикуляр на РЕ. Пусть это будет перпендикуляр НА.

∠АРН = ∠М₁М₂Т(по построению)



Из треугольника М₂М₃К


Берем с противоположным знаком, так как точка находится в четвертой четверти.
Ответ: М₃(6;-6)