Задача №102

Около окружности описана равнобедренная трапеция, основания которой равны 6 см и 24 см. Найдите радиус окружности и площадь трапеции.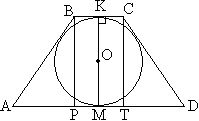

Т.к. трапеция равнобокая AB=CD.
Сделаем дополнительные построения: проведем высоты ВР, КМ, СТ.
Четырехугольник ВСТР является прямоугольником, т.к. в нем все углы прямые. Поэтому РТ=ВС=6.
Треугольники АВР и DСТ равны по катету и гипотенузе (ВР=СТ - высоты, АВ=CD - боковые ребра). Поэтому
АР=ТD=1/2(AD-BC)=1/2(24-6)=9
Теорема. Если в трапецию вписана окружность, то сумма длин оснований равна сумме длин боковых сторон.
Имеем: ВС+АD=AB+CD (AB=CD)
6+24=2AB
АВ=15
ВР²=АВ²-АР²=225-81=144
ВР=12
Радиус вписанной окружности равен половине высоты трапеции:
ОК=6
S=1/2(AD+BC)*BP=1/2(24+6)*12
S=180