Задача №106

В правильной треугольной пирамиде SABC ребро основания AB=a, боковое ребро SA=b, M - середина ребра AC. Найти: а) расстояние от точки М до плскости (SBC); б) наибольшее возможное значение угла между прямой SM и плоскостью (SBC).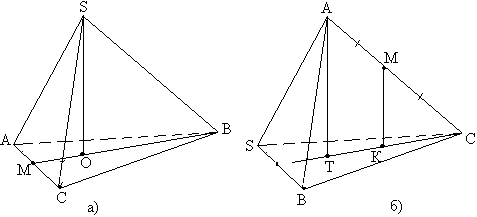

Найдем обьем пирамиды. По свойству медиан треугольника: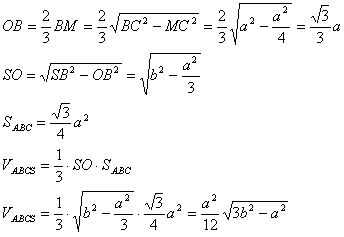

Для удобства перевернем пирамиду (рис б)
Проведем из точек А и М перпендикуляры на плоскость SBС. Они параллельны и поэтому через них можно провести плоскость причем только одну. Точка С принадлежит этой плоскости т.к. лежит на прямой АС, которая имеет в этой плоскости две точки А и М т.е. принадлежит ей.
Образованная плоскость перпендикулярна плоскости SBC т.к. проходит через прямую АТ перпендикулярную её и пересечет её по прямой СТ. Точка К принадлежит этой прямой, потому что прямая МК может пересеч плоскость SВС только по прямой СТ.
Треугольники АТС и МКС прямоугольные и подобны по острому углу. Т.к. М - середина АС получим коэффициент подобия 2. Значит MK=1/2AT.
Найдем площадь треугольника SВС, затем запишем формулу объема: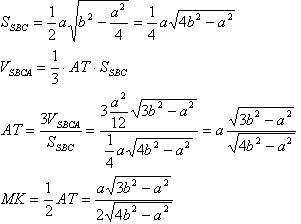


Если значение b - бокового ребра устремить к бесконечности, то этот угол будет стремиться к значению 90 градусов, но его не достигнет.