Задача №119

В правильной треугольной пирамиде сторона основания равна 3, а боковые ребра наклонены к основанию под углом 60 градусов. Найдите радиус, описанной вокруг пирамиды сферы.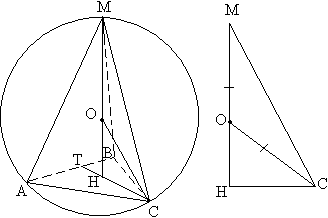

Надо отметить, что центр описанной сферы лежит на высоте пирамиды, т.к. пирамида правильная.
В треугольнике АВС определим СН как две трети от медианы СТ: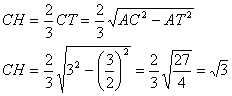

Теперь рассмотрим треугольник МНС. Здесь угол МСН равен 60 градусов, как угол между боковым ребром МС и основанием АВС. Угол НМС равен 90-60=30 градусов. МО=ОС как радиусы. Значит треугольник МОС равнобедренный. Как известно в равнобедренном треугольнике углы при основании равны: ∠ОСМ=∠ОМС=30^о
∠ОСН=∠МСН-∠МСО=60^о-30^о=30^о
Из прямоугольного треугольника ОСН определим гипотенузу ОС, используя связь тригонометрических функций в прямоугольном треугольнике: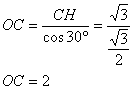