Задача №12

В ромбе ABCD с острым углом ADC из середины L стороны AD проведен перпендикуляр LM к прямой BC и перпендикуляр LN к прямой AB. Найти площадь ромба, если известно, что BM=23, BN=31.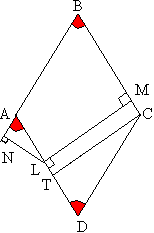
Обозначим высоту ромба за h(LM=h)
Обозначим сторону ромба за ‘х’, тогда
NA = BN – AB= 31 – x
МС = ВС – ВМ = х – 23
Т.к. точка L - середина AD, AL=x/2
Теперь из точки С параллельно LM проведем прямую CТ. Четырехугольник МСТL является параллелограммом: в нем параллельны противоположные стороны (ТС||ML - по построению, МС||LT - лежат на противоположных (параллельных) сторонах ромба). В параллелограмме противоположные стороны равны.
СТ=LM=h
LТ = МС = х-23
TD=LD-MC=x/2-(x-23)=23-x/2
Прямоугольные треугольники CTD и LAN – подобны по острому углу (∠CDT=∠NAL равны как внутренние накрестлежащие при параллельных прямых АВ и DС и секущей АD), следовательно, отношение соответствующих отрезков равно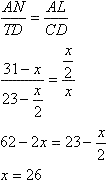

В треугольнике CTD: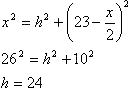

Площадь ромба можно вычислить по формуле:
S=x·h=26·24=624