| Главная Онлайн-расчеты Научный калькулятор | |
Задача №123Образующая конуса равна a, а угол при вершине осевого сечения равен α (альфа). Найдите объём конуса и его боковую поверхность.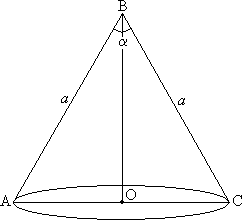 Проведем осевое сечение. Известно, что любое осевое сечение прямого кругового конуса есть равнобедренный треугольник. Поэтому высота ВО будет также и биссектриссой угла АВС, т.е. ∠ОВА=∠ОВС=α/2 Найдем ОС - радиус основания и высоту конуса ВО из прямоугольного треугольника ОВС: ВО=BC*cosα/2=a*cosα/2 ОС=BC*sinα/2=a*sinα/2 Найдем площадь боковой поверхности: Sбок=πrl=πa2*sinα/2 Найдем площадь основания: S=πr2=π(a*sinα/2)2 Найдем объем пирамиды: V=1/3Sh=1/3π(a*sinα/2)2a*cosα/2 |
|