| Главная Онлайн-расчеты Научный калькулятор | |
Задача №124Высота боковой грани правильной треугольной пирамиды равна b и составляет с плоскостью основания угол альфа. В неё вписан цилиндр, у которого h = d основания. Найти объём цилиндра.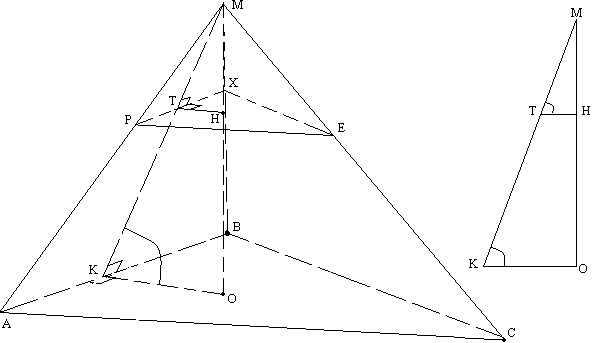 Представим себе цилиндр вписанный в правильную треугольную пирамиду. Его нижнее основание лежит в плоскости основания пирамиды, а верхнее касается всех трех боковых граней. Проведем высоту в боковой грани АВМ - МК. Т.к. пирамида правильная эта высота попадет на середину АВ. Угол между прямой и плоскостью есть угол между этой прямой и её проекцией на эту плоскость, т.е. ∠МКО=α. Теперь на высоте пирамиды возьмем точку Н. ОН - высота вписанного цилиндра. Через точку Н проведем плоскость параллельно основанию пирамиды. НТ параллельна КО т.к. они перпендикулярны одной прямой МО в плоскости МОК. Поэтому углы МТН и МКО равны. МО=МКsinα=bsinα КО=МКcosα=bcosα Надо заметить, что ТН - радиус основания цилиндра. ТН=d/2. МН=МО-НО=bsinα-d. Из подобия прямоугольных треугольников МКО и МТН по острому углу получим соотношения: 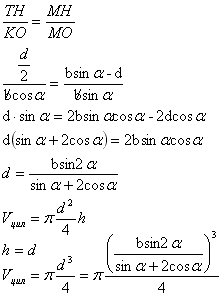
|
|