Задача №13

На сторонах параллелограмма построены квадраты. Доказать, что четырехугольник, вершинами которого являются точки пересечения диагоналей полученных квадратов, является квадратом.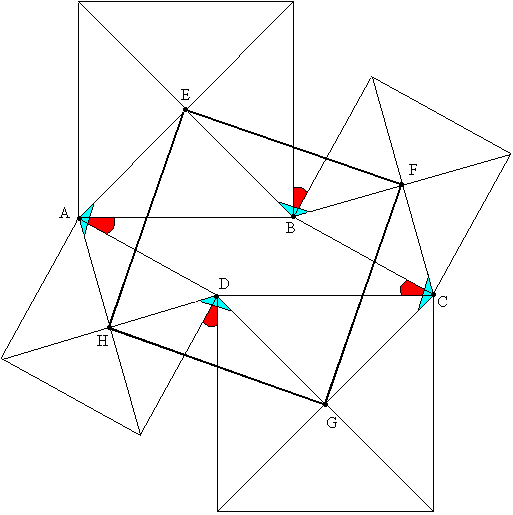
Сделаем некоторые обозначения и сразу покажем равные углы!
Стороны ЕВ, ЕА, GD и GC равны (половины диагонали большого квадрата)
Стороны FВ, ЕH, GH и FC равны (половины диагонали малого квадрата)
Углы обозначенные голубым равны сумме двух углов между диагоналями соответсвенных квадратов и их сторонами (что составляет 2 раза по 45 радусов) и красного угла. Почему же равны красные углы? Противоположные стороны параллелограмма равны, поэтому равны углы ВАD и DCВ.
Рассмотрим красный угол при вершине В. Он равен: ∠кр=360° - 90 - 90° - ∠АВС = 180° - ∠АВС
Также мы знаем, что сумма смежных углов параллелограмма равна 180°, т.е. ∠ВАD = 180° - ∠АВС
∠кр = 180° - ∠АВС = ∠ВАD
Также можно доказать и равенство последнего красного угла.
Из этого следует, что треугольники EBF, FCG, GDH и HAE равны по двум сторонам и межлежащему углу
Из равенства треугольников следует равенство соответствующих сторон EF, FG, GH и HE четырехугольника EFGH
Также следует и равенство соответственных углов, которое поможет нам в доказательстве того, что все углы четырехугольника EFGH прямые.
Докажем это на примере угла РЕF:
∠РЕF = ∠АЕВ - ∠АЕН + ∠ВЕF
∠АЕН = ∠ВЕF из равенства треугольников АЕН и ВЕF, а угол АЕВ есть угол между диагоналями квадрата, т.е. прямой, поэтому
∠РЕF = 90°
В четырехугольнике EFGH все стороны равны и все углы прямые, следовательно, этот четырехугольник - квадрат!