Задача №131

Прямые, содержащие биссектрисы внутренних углов при вершинах В и С треугольника АВС, пересекаются в точке О. Найдите угол ВОС, если угол при верщине А равен альфа.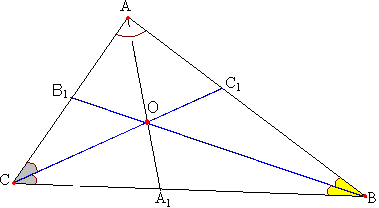

Обозначим ∠ВОС за х. Тогда из треугольника ВОС:
х+∠С/2+∠B/2=180°, откуда
∠С/2+∠B/2=180°-х.
Умножим обе части неравенства на 2:
∠С+∠B=360°-2х. (1)
Из треугольника АВС:
∠А+∠В+∠С=180°, откуда
∠В+∠С=180°-∠А. (2)
Приравнивая правые части уравнений (1) и (2), получаем:
360°-2х=180°-∠А, откуда
2х=180°+∠А
х=90°+∠А/2 или
∠ВОС=90°+∠α/2