| Главная Онлайн-расчеты Научный калькулятор | |
Задача №132Из центра О ромба ABCD проведён к плоскости ромба перпендикуляр ОМ. Вычислить расстояние от точки М до вершин ромба, если ОМ = 3 корня из 3, AB=12 и ∠BAD=60 градусов.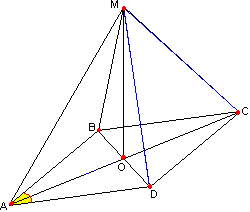 Другими словами нам требуется найти боковые ребра пирамиды. Нужно напомнить, что центр ромба - это точка пересечения его диагоналей. Точкой пересечения диагонали делятся пополам. Диагонали ромба перпендикулярны. Т.к. МО перпендикулярен плоскости основания, то он перпендикулярен любой прямой в этой плоскости, поэтому треугольники МОА, МОВ, МОС и MOD прямоугольные, причем, треугольник МОА = треугольнику МОС (по двум катетам МО - общая, АО=ОС - половины диагонали) и треугольник МОВ = треугольнику МОD (по двум катетам МО - общая, BО=ОD - половины диагонали). Поэтому равны соответственно и их гипотенузы: МА=МС и МВ=MD. В треугольнике АВD стороны АВ и АD равны (стороны ромба), поэтому он равнобедренный треугольник с углом при вершине 60 градусов. А это значит, что все углы этого треугольника равны 60 градусов, т.е. треугольник равносторонний и BD=АВ=12. OD=1/2BD=6. Из прямоугольного треугольника АОD: 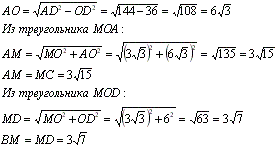
|
|