Задача №134

Стороны треугольника равны 25,29,36. Точка вне плоскости треугольника удалена от каждой из сторон на 17 см. Найдите расстояние от данной точки до плоскости треугольника.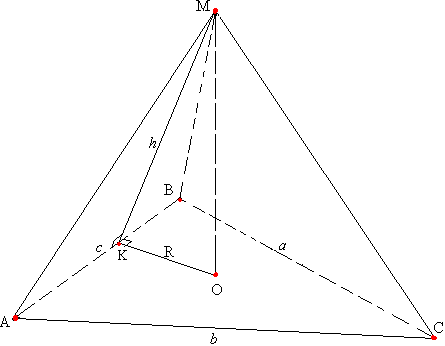

По сути, дело имеем с пирамидой, у которой данная точка (обозначим её за М) - вершина, а данный треугольник (АВС) - основание. Найти надо высоту МО
Воспользуемся теоремой: если все апофемы (высоты боковых граней) пирамиды равны, то высота такой пирамиды падает в центр вписанной в основание окружности. Утверждаем, что точка О - основание высоты МО является также и центром вписанной в треугольник АВС окружности.
Проведем радиус ОК. Он перпендикулярен стороне АВ по свойству радиуса, проведенного в точку касания. Теперь соединим точки К и М. КМ перпендикулярна АВ по теореме о трех перпендикулярах. Таким образом, мы посторили апофему КМ.
Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулами: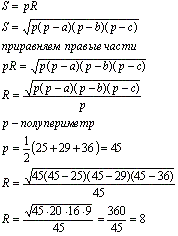

Теперь из прямоугольного треугольника КОМ найдем МО: