Задача №138

В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого = 2а, а прилежащий угол = 30 градусов. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45 градусов. Нужно найти объём конус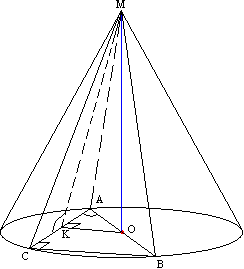а.
Рассмотрим треугольник АВС - основание. Вспомним: Если вписанный в окружность угол равен 90 градусов, то он опирается на диаметр. Поэтому гипотенуза АВ является диаметром. Из центра окружности - точки опустим перпендикуляр на катет АС. Точка К разделит АС пополам по теореме Фалеса. Поэтому АК=а.
Из прямоугольного треугольника АОК: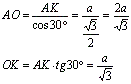

Соединим точки К и М. МК перпендикулярна АС по теореме о трех перпендикулярах. Угол МКО есть линейный угол двугранного угла между плоскостью АСМ и плоскостью основания. Треугольник МОК прямоугольный и равнобедренный (острый угол 45 градусов), поэтому: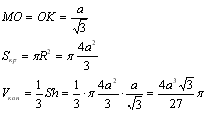