Задача №161

Докажите, что в трапеции середины оснований и точка пересечения диагоналей лежат на одной прямой.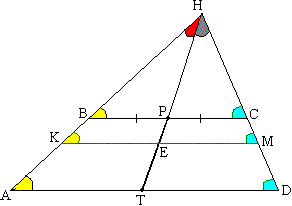
Возьмём некую трапецию АВСD. Продолжим её боковые стороны до пересечения. Точку пересечения обозначим за Н. В треугольнике ВНС проведем мединану НР и продолжим её до пересечения с AD. Точку их пересечения обозначим за Т.
Треугольники ВРН и АТН подобны по двум углам (∠ВНР - общий, ∠НВР=∠НАТ - соответственные), поэтому:
НР:НТ=ВР:АТ
Треугольники СРН и DТН подобны по двум углам (∠СНР - общий, ∠НСР=∠НDТ - соответственные), поэтому:
НР:НТ=CР:DТ, поэтому
ВР:АТ=CР:DТ, но ВР=СР (по построению), поэтому АТ=DТ, т.е. НТ является медианой. Таким образом, можно доказать, что медиана НР будет являться медианой (проходить через середины сторон) для части любой прямой параллельной ВС заключенной между прямыми НВ и НС. Например, точка Е будет серединой прямой КМ. Заметим, что точки Р и Т - середины оснований трапеции АВСD.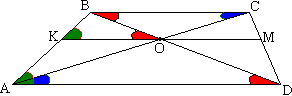
Теперь рассмотрим трапецию АВСD и пусть прямая КМ проходит через О - точку пересечения диагоналей, параллельно основаниям. Пусть AD=a, ВС=b. Если параллельные прямые пересечены третей, то соответствующие и накрест лежащие углы равны. Основания трапеции параллельны, следовательно, ∠BDA=∠CBD и ∠CAD=∠CBA и по второму признаку подобия подобны треугольники ВОС и DОА. Следовательно, ВО:OD=BC:AD, т.е. ВО:OD=b:a.
Отсюда находим, что ВО:BD=b/(a+b). (1)
Прямая КМ параллельна основанию AD, поэтому ∠ВКО=∠ВАD и ∠ВОК=∠BDA, треугольники КВО и АВD также подобны и КО:AD=ВО:BD. Отсюда, учитывая (1), получаем КО=аb/(a+b). Аналогично устанавливаем, что МО=аb/(a+b), т.е. КО=МО или точка О - середина КМ.
Значит, точка О принадлежит и прямой РТ (рисунок 1). На прямой РТ лежат все три из необходимых точек. Ч.т.д.