| Главная Онлайн-расчеты Научный калькулятор | |
Задача №164Дана правильная четырехугольная пирамида МABCD. Диагональ основания AC равна 6 корней из 2. Угол между боковыми гранями пирамиды и основанием равен 60 градусов. Найти боковую поверхность пирамиды! 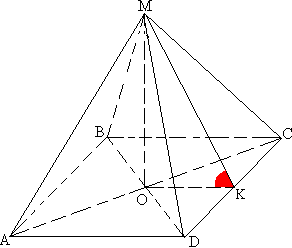 Раз пирамида правильная, значит, АВСD - квадрат. Как известно, диагональ квадрата в корень из двух раз больше стороны. Поэтому АВ=6.
Раз пирамида правильная, значит, АВСD - квадрат. Как известно, диагональ квадрата в корень из двух раз больше стороны. Поэтому АВ=6.Из точки пересечения диагоналей основания опустим перпендикуляр ОК на CD. Теперь соединим точки М и К. Угол МКО являеся линейным для двугранного угла между боковой гранью МСD и основанием АBCD и равен он по условию 60°. Из прямоугольного треугольника МКО найдем МК: МК=ОК/cos60°, где ОК - половина стороны основания ОК=3 МК=6 Площадь боковой поверхности пирамиды есть учетверенная площадь треугольника CMD, т.к. пирамида правильная и все боковые грани - равные равнобедренные треугольники. Sбок=4SCMD=4 * 1/2 * MK * СD=72 (квадратных единиц). |
|