Задача №167

У четыреугольника EFST ∠Т=50°, угол EST - прямой, ES - бисектриса угла Е, EF=FS. Доказать, что EFST-трапеция. Найти угол F.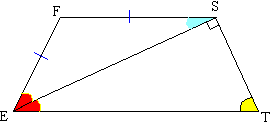
EF=FS, следовательно, треугольник EFS равнобедренный. Из теоремы: в ранобедренном треугольнике углы при основании равны следует, что
∠FES=∠ESF. Также известно ∠FES=∠ТES, поэтому ∠ТES=∠ESF.
Теорема: если накрестлежащие углы равны, то прямые параллельны. Для прямых ЕТ и FS углы ∠ТES и ∠ESF являются накрестлежащими, поэтому они параллельны. Четырехугольник EFST трапеция по определению.
Если так, то углы FST и STE являются внутренними односторонними, и их сумма равна 180°:
∠FST=180°-∠STE=180°-50°=130°
∠FSЕ=∠FST-∠ЕST=130°-90°=40°
∠FSЕ=∠TES=40°
∠FEТ=2∠TES=80°
Углы EFS и FET являются внутренними односторонними, и их сумма равна 180°:
∠EFS=180°-∠FET=180°-80°=100°