Задача №168

Точки А, В, С и Д не лежат в одной плоскости. Середины ДА соединена с серединой ВС, Середина ДС - с серединой ВА и середина ДВ - с серединой АС. Доказать, что соединяющие прямые пересекаются в одной точке.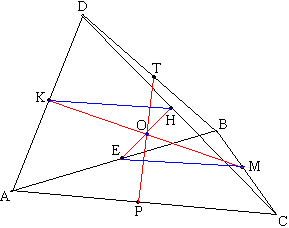
Обозначим (еще не обозначенные) точки как показано на рисунке. Соединим точки К и Н, Е и М соответственно. КН является средней линией в треугольнике АСD и (по теореме) параллельна АС. Также в треугольнике АВС ЕМ параллельна АС. Изпользуем теорему: если две прямые (в пространстве) параллельны третей прямой, то они параллельны между собой. Поэтому КН параллельна ЕМ. Через пару параллельных прямых в пространстве можно провести плоскость и при том только одну. Поэтому прямые КН и ЕМ определяют плоскость, а прямые КМ и ЕН пересекаются в точке О.
Таким же образом докажем, что пересекаются прямые ТР и ЕН, КМ и ТР соответственно.
Прямая ТР (не лежит) пересекает плоскость КЕМН, т.е. имеет с ней одну общую точку. Также прямая ТР пересекает две прямые этой плоскости ЕН и КМ. Поэтому ТР может проходить только через точку О (т.е. и пересекает плоскость в одной точке, и пересекает прямые ЕН и КМ).
Таким образом, прямые ЕН, КМ и ТР проходят через одну точку О, ч.т.д.