Задача №17

Даны вершины треугольника: А (-10;-13), В (-2;3), С (2;1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.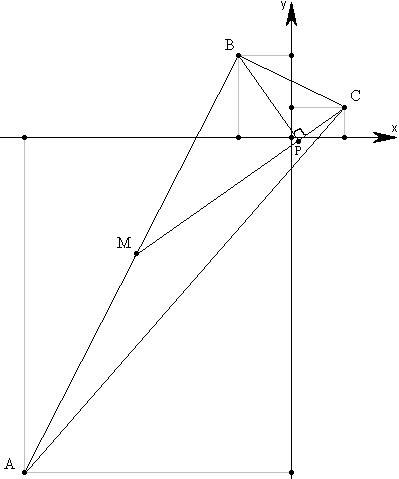

Найдем координаты точки М (она является серединой отрезка АВ)

М(-6;-5)

Найдем уравнение прямой. Для этого  запишем уравнения для точек М и С

1=2k+d

-5=-6k+d

k=3/4; d=-1/2

Теперь найдем уравнение отрезка ВР (по заданию ВР перпендикулярен МС, то есть угловой коэффициент находится соотношением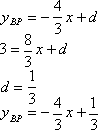
k=-1/k_MC=-4/3)
Dля нахождения свободного чрена подставим в уравнение значения точки В

Для нахождения точки Р приравняем уравнения прямых МС и ВР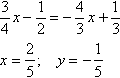

И теперь по координатам точек найдем длину