Задача №178

Периметр ромба равен 20см, а его площадь 20 см². Найти длину его меньшей диагонали.
Ищем BD.
Запишем формулу периметра ромба:
P=4a=20
a=5
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Рассмотрим прямоугольный треугольник АОВ:
ОА²+ОВ²=a²=25(1)
BD=2ОВ, АС=2ОА
Площадь ромба равна половине произведения его диагоналей:
S=1/2 * АС * BD
S=1/2 * 2ОА * 2ОВ
2ОА * ОВ=20
ОА * ОВ=10
ОА=10/ОВ
Подставим полученное выражение в формулу (1)
100/OB²+ОВ²=25
ОВ⁴-25ОВ²+100=0, ОВ не равно нулю.
ОВ²=х
х²-25х+100=0
х₁=20; х₂=5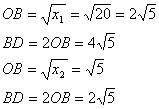

меньший ответ и будет результатом