Задача №195

Найдите площадь прямоугольника, если одна из его сторон равна 5см, а угол между диагоналями равен 60 градусов.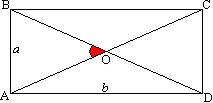
Диагонали прямоугольника равны и точкой пересечения делятся пополам. Поэтому, ОА=ОВ=ОС. Треугольник АОВ - равнобедренный (по определению). Угол при его вершине равен 60 градусов, а значит и при основании углы по 60 градусов (120/2). Т.е. этот треугольник - равносторонний. ОА=ОВ=АВ
Противоположные стороны прямоугольника равны. Обозначим меньшую за а, а большую за b.
Случай 1. а=5, т.е. ОА=ОВ=АВ=5. АС=2ОА=10.
Площадь прямоугольника равна половине произведения квадрата диагонали и синуса угла между его диагоналями.
S=1/2 * 10² * sin60°
S=1/2 * 100 * (корень из 3)/2
S=25 корней из 3

Случай 2. b=5. В треугольнике АВС ВС=5, ∠ВАС=60°.
a=b * ctg60°=5 * (корень из 3)/3
S=a * b=(25 корней из 3)/3