| Главная Онлайн-расчеты Научный калькулятор | |
Задача №206Правильная четырехугольная призма, объем которой 65 дм3, описана около шара. Вычислите отношение площади полной поверхности призмы и объема шара 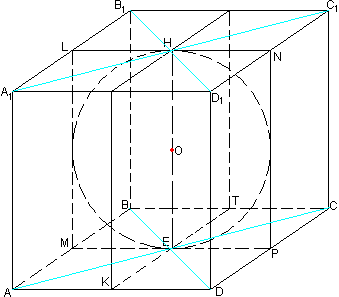 Призма называется правильной, если её основаниями являются правильные многоугольники, а боковые ребра перпендикулярны основанию. Правильным четырехугольником является квадрат. Точка пересечения диагоналей квадрата является его центром, а также центром вписанной в него окружности. Докажем этот факт. хотя это доказательство наврядли будут спрашивать и его можно опустить
Призма называется правильной, если её основаниями являются правильные многоугольники, а боковые ребра перпендикулярны основанию. Правильным четырехугольником является квадрат. Точка пересечения диагоналей квадрата является его центром, а также центром вписанной в него окружности. Докажем этот факт. хотя это доказательство наврядли будут спрашивать и его можно опустить 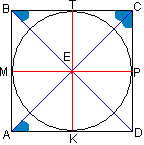 Как частный вид параллеограмма, прямоугольника и ромба квадрат обладает их свойствами: диагонали равны и делятся точкой пересечения пополам, и являются биссектрисами углов квадрата. Через точку Е проведем прямую ТК параллельно АВ. АВ перпендикулярна ВС, значит и ТК тоже перпендикулярна ВС (если одна из двух параллельных прямых перпендикулярна какой-либо третей прямой, то и вторая параллельная прямая перпендикулярна этой (третей) прямой). Таким же образом проведем прямую МР. Прямоугольные треугольникик ВЕТ и АЕК равны по гипотенузе и острому углу (ВЕ=АЕ - половины диагоналей, ∠ЕВТ=∠ЕАК - половины прямого угла), значит, ЕТ=ЕК. Таким же образом докажем, что ЕМ=ЕР. А из равенства треугольников СЕР и СЕТ (тот же признак) увидим, что ЕТ=ЕР, т.е. ЕТ=ЕР=ЕК=ЕМ или просто сказать, что точка М равноудалена от сторон квадрата, а это и есть необходимое условие для того, чтобы признать её центром вписанной в этот квадрат окружности. Как частный вид параллеограмма, прямоугольника и ромба квадрат обладает их свойствами: диагонали равны и делятся точкой пересечения пополам, и являются биссектрисами углов квадрата. Через точку Е проведем прямую ТК параллельно АВ. АВ перпендикулярна ВС, значит и ТК тоже перпендикулярна ВС (если одна из двух параллельных прямых перпендикулярна какой-либо третей прямой, то и вторая параллельная прямая перпендикулярна этой (третей) прямой). Таким же образом проведем прямую МР. Прямоугольные треугольникик ВЕТ и АЕК равны по гипотенузе и острому углу (ВЕ=АЕ - половины диагоналей, ∠ЕВТ=∠ЕАК - половины прямого угла), значит, ЕТ=ЕК. Таким же образом докажем, что ЕМ=ЕР. А из равенства треугольников СЕР и СЕТ (тот же признак) увидим, что ЕТ=ЕР, т.е. ЕТ=ЕР=ЕК=ЕМ или просто сказать, что точка М равноудалена от сторон квадрата, а это и есть необходимое условие для того, чтобы признать её центром вписанной в этот квадрат окружности.Рассмотрим прямоугольник АВТК (этот четырехугольник является прямоугольником, т.к. все углы в нем прямые по построению). В прямоугольнике противоположные стороны равны - АВ=КТ (нужно отметить, что КТ - диаметр основания) - это значит, что сторона основания равна диаметру вписанной окружности. Проведем плоскости через параллельные (две прямые, перпендикулярные одной и той же плоскости, параллельны) АА1, СС1 и ВВ1 и DD1 соответственно (параллельные прямые определяют плоскость притом только одну). Плоскости АА1С1С и ВВ1D1D перпендикулярны основанию ABCD, т.к. проходят через прямые (боковые ребра) перпендикулярные ему. Из точки Н (пересечения диагоналей) в плоскости АА1С1С перпендикуляр к основанию ABCD. Затем проделаем тоже самое в плоскости ВВ1D1D. Из теоремы: если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости, - получаем, что этот перпендикуляр должен лежать и в плоскости АА1С1С и в плоскости ВВ1D1D. Это возможно лишь в том случае, если этот перпендикуляр совпадает с линией пересечения этих плоскостей - НЕ. Т.е. отрезок НЕ является прямой, на которой лежит центр вписанной окружности (т.к. НЕ равноудалена от плоскостей боковых граней, а это в свою очередь следует из равноудаленности точек Е и Н от вершин соответсвующих оснований (по доказанному: точка пересечения диагоналей равноудалена от сторон квадрата), а из того, что НЕ перпендикулярна основаниям можно заключить, что НЕ - диаметр шара. Теорема. В правильную призму можно вписать шар тогда и только тогда, когда её высота равна диаметру окружности, вписанной в основание. Ну а в нашу призму уже вписан шар, значит её высота равна диаметру окружности, вписанной в основание. Если обозначить сторону основания за а, а высоту призмы за h, то пользуясь этой теоремой, заключаем а=h и тогда объем призмы найдется так: 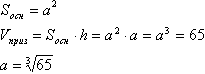 Далее используя то, что высота равна диаметру вписанного шара и стороне основания призмы, найдем радиус шара а затем его объем: 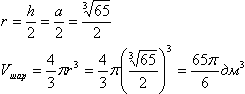 Нужно сказать, что боковые ребра равны высоте (отрезки параллельных прямых, заключенные между параллельными плоскостями равны), а раз высота равна стороне основания, то вообще все ребра призмы равны между собой, а все грани по сути являются квадратами с площадью а2. По сути такая фигура называетс кубом - частным случаем параллелепипеда. Осталось найти полную поверхность куба и соотнести ее с объемом шара: 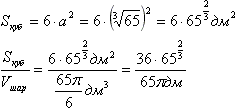
|
|