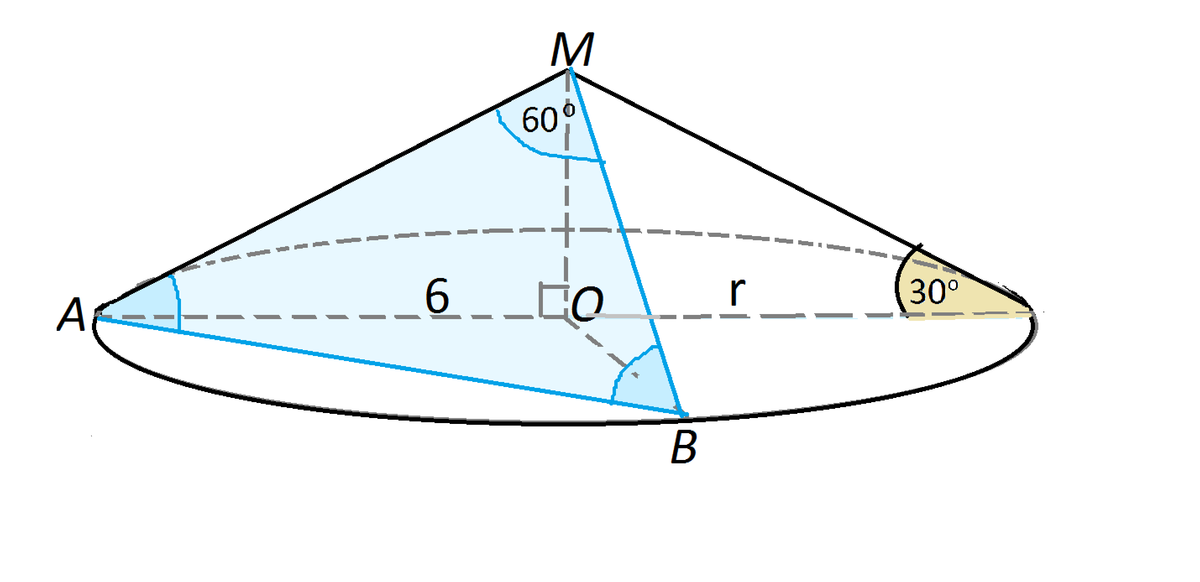
Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;
б) площадь боковой поверхности конуса.

Решение:

Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Плоскость сечения ограничена по бокам двумя образующими. 
Следовательно, это равнобедренный треугольник.
Угол между образующими = 60°.
Следовательно, сечение представляет из себя равносторонний треугольник. Площадь равностороннего треугольника можно найти несколькими способами. 
а) По классической формуле
S=ah:2
б) По формуле Герона
в) По формуле площади для равностороннего треугольника, т.е. квадрата стороны, умноженной на синус угла между сторонами, деленному на два. 
S=(a?√3):4 . 
Найдем образующую, которая образует с плоскостью основания угол 30°
АМ=МО/соs(30°)
АМ=6:(√3?2)=4√3 см
Sсеч=(4√3)?*√3):4=48√3):4=12√3 см?

б) Площадь боковой поверхности конуса.
Боковая площадь поверхности круглого конуса равна произведению половины окружности основания на образующую S=0,5 C* l=? r l,
 где С- длина окружности основания, l-образующая
Sбок=? 6*4√3=24√3 см?