Задача №22

Найдите площадь боковой поверхности правильной четырёхугольной пирамиды, если диагональное сечение пирамиды - прямоугольный треугольник, площадь которого равна 32 см в квадрате.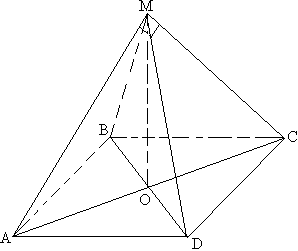
Прежде всего надо сказать, что в правильной пирамиде в основании лежит правильный многоугольник (в данном случае квадрат) и все боковые грани такой пирамиды равны между собой (пирамида). Поэтому оба диагональных сечения являются равными равнобедренными треугольниками (по трем сторонам).
Рассмотрим треугольник АМС: он прямоугольный (по данным), его площадь известна и обозначим АМ=МС=а: теперь это запишем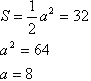

Треугоники АМС и АВС равны по гипотенузе и осрому углу (АС - общая, а острые углы по 45 градусов, т.к. оба треугольника равнобедренные), поэтому АВ=а=8
Мы определили, что все боковые грани пирамиды – правильные треугольники со стороной 8, значит, площадь боковой поверхности найдется по формуле: