| Главная Онлайн-расчеты Научный калькулятор | |
Задача №230Плоскости α и β пересекаются под некоторым углом. Точка А принадлежит плоскости α и отстоит от плоскости β на 10 см, а от линии пересечения плоскостей - на 20 см. Найти угол между плоскостями.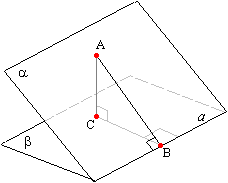 Из точки А опустим перпендикуляр на плоскость β. Отрезок АС есть расстояние от точки А до этой плоскости и равен 10. В плоскости α из точки А опустим перпендикуляр на прямую а. Отрезок АВ является расстоянием между точкой А и линией пересечения плоскостей α и β, поэтому равен 20. Соединим точки В и С. Прямая ВС перпендикулярна прямой а по теореме о трех перпендикулярах (обратная). Угол АВС является линейным углом двугранного угла между плоскостями α и β по определению. Именно его-то нам и нужно найти! АС, как перпендикуляр к плоскости β перпендикулярен любой прямой в этой плоскости в том числе и прямой ВС по определению, поэтому треугольник АВС прямоугольный. Значит, мы можем поизвести следующие действия: 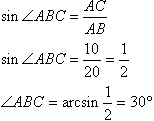
|
|