Задача №240

На сторонах AB и BC параллелограмма построены квадраты ABMN и BCEF. Докажите, что DE=DN!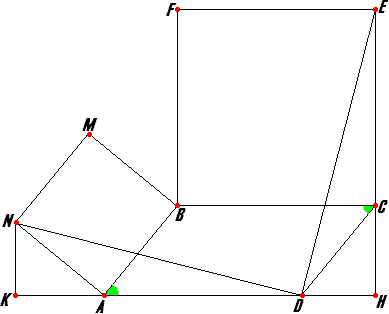 Сделаем дополнительные построения: опустим перпендикуляры из вершин N и С на прямую AD.
1. Докажем, что отрезки АК и СН равны
1.1. У параллелограмма есть такое свойство, что противоположные стороны равны, поэтому: АВ=CD. Т.к. АВMN - квадрат, АВ=AN
1.2. Вспомним еще одно свойство параллелограмма: противоположные углы параллелограмма равны, поэтому ∠BАD=∠BСD (1)
Также a) ∠BAD=180°-∠BAN-∠KAN=180°-90°-∠KAN
∠BAD=90°-∠KAN
б) ∠BCD=90°-∠HCD
Подставив а) и б) в выражение (1) получим:
90°-∠KAN=90°-∠HCD, откуда
∠KAN=∠HCD
Из рассуждений 1.1 и 1.2 можно понять, что прямоугольные треугольники KAN и HCD равны по гипотенузе и острому углу. Поэтому АК=СН и KN=DH как катеты этого треугольника.

2. Докажем, что DE=DN
2.1. Еще раз вспомним свойство: противоположные стороны параллелограмма равны - AD=BC. Т.к. BCEF - квадрат, ВС=СЕ. Т.е. AD=BC=СЕ.
Используя выводы пунктов 1. и 2.1 заключим:
KD=AK+AD=CH+CE=EH
2.2 Рассмотрим прямоугольные треугольники NKD и EHD. Используя выводы пунктов 1. и 2.1 можно понять, что они равны по двум катетам (KN=DH и KD=EH), а значит равны и их гипотенузы:
DE=DN, что и требовалось доказать!