Задача №243

Через вершину прямого угла С треугольника АВС проведена прямая l перпендикулярно плоскости треугольника АВС. Плоскость, проходящяя через сторону АВ под углом 45 градусов к плоскости АВС, пересекает прямую l в точе D. Найдите площадь треугольника АВD, если ВС=2, угол СВА=30 градусам.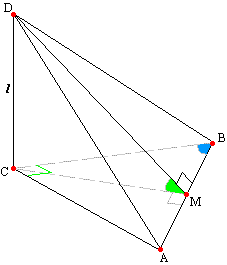

В треугольнике АВС проведем высоту СМ. Из прямоугольного треугольника ВСМ СМ=ВС * sin30°=1. Соединим точки М и D. DМ перпендикулярна AВ по теореме о трех перпендикулярах.
Угол CМD является линейным углом двугранного угла между плоскостями АВС и DAВ , поэтому ∠DМC=45°. Ребро CD перпендикулярно основанию, поэтому перпендикулярно любой прямой плоскости основания (по определению), т.е. треугольник DCМ прямоугольный.

Итак, осталось выполнить только следующие действия:
1. Найдем гипотенузу DM из прямоугольного треугольника DCМ;
2. Найдем гипотенузу АВ из прямоугольного треугольника АВС;
3. Найдем площадь треугольника АВD.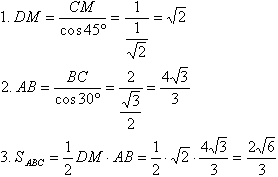