Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2см, а диаметр окружности равен 4 см.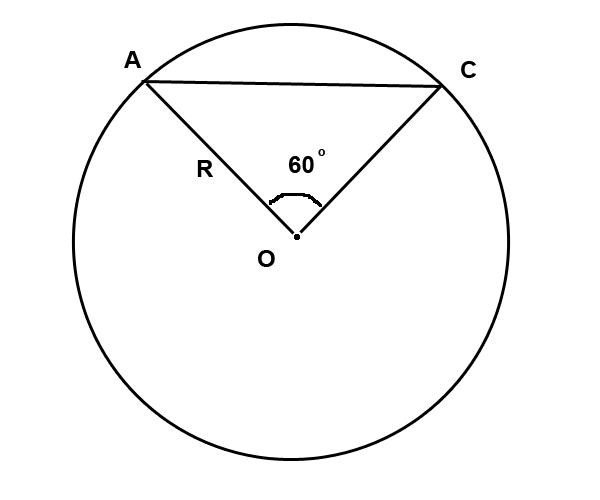

Решение:

Пусть О – центр окружности, АС – данная хорда. АС = 2 см

Радиус окружности равен половине диаметра, поэтому радиус окружности равен:

R = OA = OC = 4/2 = 2 см

OA = OC = АС = 2 см.

Поэтому треугольник ОАС – равносторонний, а значит угол АОС = 60 градусов.(центральный угол)

Площадь кругового сектора вычисляется по формуле:

Sкс = pi*R^2*альфа360 градусов

где R – радиус круга, а альфа - градусная мера соответствующего центрального угла.

Sкс = pi*2^2*60 градусов 360 градусов= 23*pi см²

Площадь треугольника АОС равна АС^2*корень(3)4=

=2^2 *корень(3)4=корень(3) см².

Площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой = Площадь кругового сектора - площадь треугольника АОС

Площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой =

= 23*pi - корень(3) см².

Ответ: 23*pi-корень(3) см².