Вписанная в трапецию окружность делит одну из боковых сторон на отрезки 4см и 9см. Найдите площадь трапеции, если одно из оснований равно 7см.

Решение:

Пусть АВСD - данная трапеция, K, L, M, N, - точки касания вписанной в трапецию окружности, соотвественно со сторонами: AB, BC, CD, AD. AN=4, DN=9, AB=7.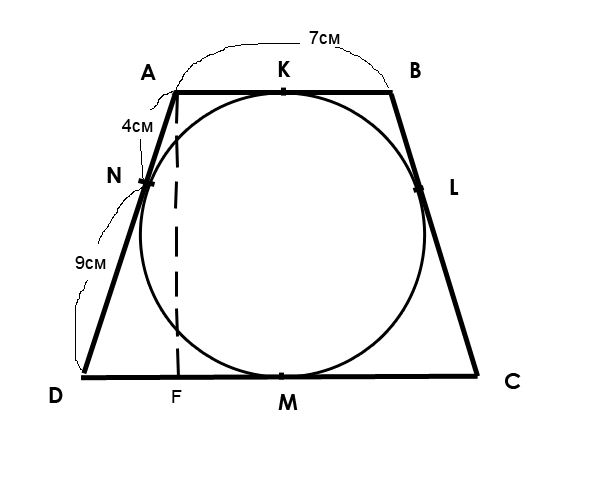

По свойству, что касательные проведенные к окружности из одной точки имеют равные длины:

AN = AK = 4BK = BL = 5CL = CMDN = DM = 9BK = AB - AK = 7 - 4 = 3

Проведем высоту AF к основанию CD.
AF = KMAK = FM = 4DF = DM - FM = 9 - 4 = 5AD = AN + DN = 4 + 9 = 13

По теореме Пифагора:

AF² = AD² - DF² = 13² - 5² = 12

Проведем высоту BH к основанию AD:

BH = AF = 12KB = MH = 3.

Пусть CL = CM = xCM = x - 3

Тогда по теореме Пифагора: 12² = (3+x)² - (x-3)²

144 = 9 + 6x + x² - x² + 6х - 9

144 = 12x

x = 144/12 = 12

СD = DM + MH + CH = 9 + 12 = 21

Площадь трапеции ABCD равна: (AB+CD)2*AF=(7+21)2*12=168 см²

Ответ: 168 см²