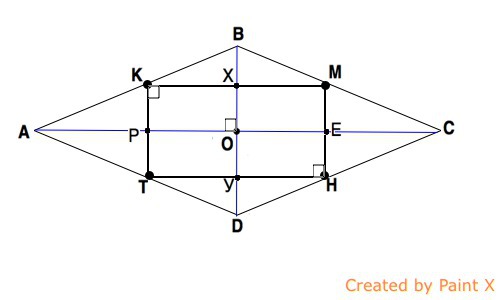
Докажите что если вершины прямоугольника являются серединами сторон некоторого параллелограмма, то этот параллелограм - ромб

Решение:

Дано: АВСD - параллелограмм,   АК=КВ, ВМ=МС, СН=НD, DТ=ТА 

КМНТ - прямоугольник. 

КМ соединяет середины  сторон   ? АВС  ? КМ его средняя линия и параллельна АС  . 

КТ соединяет середины сторон ? АВD, ? КТ его средняя линия и параллельна ВD (свойство) . 

Аналогично ТН¦АС и МН¦ВD 

Лемма: 

Если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к этой третьей  прямой.

КТ¦ВД

 КТ?ТН,?   ВД?ТН; (1)

ТН¦АС 

ТН?ВД?  АС?ВД (2)

Если диагонали параллелограмма  пересекаются под прямым углом (2) , этот параллелограмм - ромб.

Вариант решения. 

Обозначим точки пересечения диагонали АС параллелограмма АВСД со сторонам КТ и МН буквами Р и Е, а точки пересечения  диагонали ВД со сторонами КМ и ТН буквами Х и У соответственно. 

Диагонали АВСД  делят стороны  ТКМН пополам. ? 

РКХО=ХМЕО=ЕНУО=УТРО  и являются параллелограммами ?

их углы при О, противолежащие прямым углам при вершинах прямоугольника КМНТ, тоже прямые. ?

АС и ВД пересекаются в точке О про углом 90?. 

Если диагонали параллелограмма пересекаются под прямым углом, этот параллелограмм - ромб, что и требовалось доказать.