Задача №28

Вне плоскости Альфа распложен треугольник ABC, у которого медианы AA₁ и BB₁ параллельны плоскости Альфа. Через вершины B и C треугольника проведены параллельные прямые, которые пересекают плоскость Альфа в точках E и F. Докажите, что ECBF параллелограмм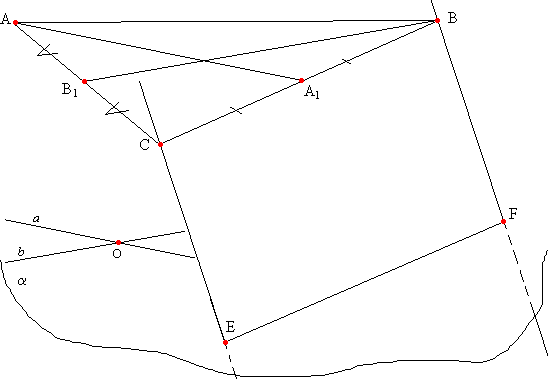
В плоскости α возьмем произвольную точку О. Через точку О и прямые сначала AA₁, затем BB₁ проведем плоскости (прямая и точка определяют плоскость, причем только одну). Если две плокост имеют общую точку, то они имеют и общую прямую, проходящую через эту точку. Пусть эти плоскости пересекли плоскость α по прямым a и b, как показано на рисунке. Можно заключить, что а || AA₁ и b || BB₁. Например, рассмотрим первую пару. Если бы прямая AA₁ пересекала бы прямую а, то она бы имела общую точку с плоскостью α, чего быть не может, т.к. прямая AA₁ параллельна плоскости альфа по данным.
Вспомним, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны (признак параллельности плоскостей). Поэтому плоскости альфа и плоскость треугольника АВС параллельны.
Как известно, отрезки параллельных прямых, заключенные между двумя параллельными плоскостями равны. Другими словами в четырехугольнике ECBF стороны EC и BF – противоположны, параллельны и равны.
Признак: если в четырехугольнике пара противоположных сторон равны и параллельны, то такой четырехугольник - параллелограмм.