Задача №3

Составить уравнение сторон треугольника АВС, если даны одна из его вершин А(1;3) и уравнение двух медиан х - 2у + 1=0 и у-1=0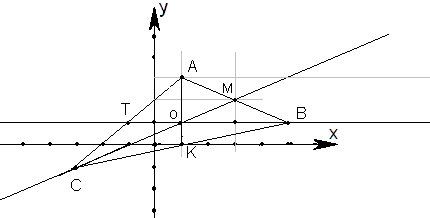


Для начала выразим у: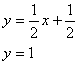

Эти графики пересекаются в точке О (1;1) Это точка пересечения этих медиан.
Как известно все медианы пересекаются в одной точке. Поэтому мы можем провести медиану из вершины А.
Эта медиана параллельна оси у и соответственно перпендикулярна оси х так, как две её точки А и О имеют одинаковую абсциссу.
Также известно, что медианы пересекаясь, делятся в отношении 2:1 считая от вершины.
Расстояние от вершины до точки пересечения АО = 2. Пусть точка пересечения медианы с противоположной стороной ВС – точка К, тогда ОК = 1, то есть точка К лежит на оси х и имеет координаты К(1;0). Известно, что вершины лежат соответственно на двух остальных медианах. Возьмем некоторые точки В и С на соответственно разных медианах. Мы знаем, что точка К делит ВС пополам, то есть ВК = СК. Соединим вершины и обозначим точки пересечения сторон и медиан.
Ну про точку М трудно что-либо сказать, а вот точка Т (как лежащая на прямой у = 1)  имеет ординату 1. Поэтому можно записать формулу середины отрезка для точек А и С, причем запишем только для координаты у: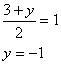

где у – ордината точки С. Мы знаем, что точка С лежит на медиане заданной уравнением функции х - 2у + 1 = 0, подставим значение у в это уравнение и найдем абсциссу точки С. х + 2 +1=0; х = -3. Значит, С(-3;-1)
Для нахождения координат точки В запишем уравнение середины отрезка для точек С и В, обозначив х и у координаты точки В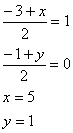

Итак В(5;1)
Введем  следующие обозначения:
Прямая, содержащая сторону 1) АВ – у₁ =k₁x + b₁
2) АC – у₂ =k₂x + b₂
3) CВ – у₃ =k₃x + b₃
Составим два уравнения соответственно  для точки А и точки В (5;1)
 3 = k₁ + b₁
1 = 5k₁ + b₁, откуда k₁ = -1/2      и b₁ = 7/2
Составим два уравнения соответственно  для точки А(1;3)  и точки C(-3;-1)
3 = k₁ + b₁
-1 = -3k₁ + b₁, откуда k₁ = 1       и b₁ = 2
1)      Составим два уравнения соответственно  для точки C и точки В
-1 = -3k₁ + b₁,
1 = 5k₁ + b₁, откуда k₁ = 1/4      и b₁ = -1/4      

Ответ: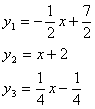