Точка М равноудалена от всех вершин равнобедренного прямоугольного треугольника АСВ (<С=90?), АС=ВС=4 см. Расстояние от точки М до плоскости треугольника равно 2v3 см.

1) Докажите, что плоскость АМВ перпендикулярна плоскости АВС.

2) Какой угол плоскость ВМС составляет с плоскостью АВС?

3) Найдите угол между МС и плоскостью АВС.

4) Найдите расстояние от точки Е-середины стороны АС до плоскости ВМС.

Решение:

1. Поскольку М равноудалена от  вершин АВС, то её проекция О на поскость ABC тоже равноудалена от вершин, то есть О - центр окружности, описанной вокруг прямоугольного треугольника АВС. Поэтому О лежит точно в середине гипотенузы.

СО перпендикулярно АВ, поскольку треугольник равнобедренный, и медиана одновременно - высота. МО перпендикулярно СО, поскольку МО вообще перпендикулярно плоскости АВС. Поэтому плоскости АВС и АМС взамино перпендикулярны, а угол МОС - их двугранный угол, равный, само собой, 90 градусов. Далее "пп" означает "перпендикулярно" "тр" - "треугольник" "птр" - прямоугольный "тр"

2. ОР пп АВ; СР = РВ = РО = 2; МО = 2*√(3); Поэтому tg(MPO) = 1/√(3); 

Угол МРО = 60 градусам.

3. В птр OMC СО = АС*sin(45) = 2*√(2); MO = 2*√(3); tg(MCO) = √(3/2);

4. Достаточно найти расстояние от точки О до плоскости МСВ, поскольку ЕО параллельно ВС, а - следовательно, и всей плоскости ВМС.

К - высота в птр ОМР,

ОК = ОР*sin(MPO) = 2*√(3)/2 = √(3)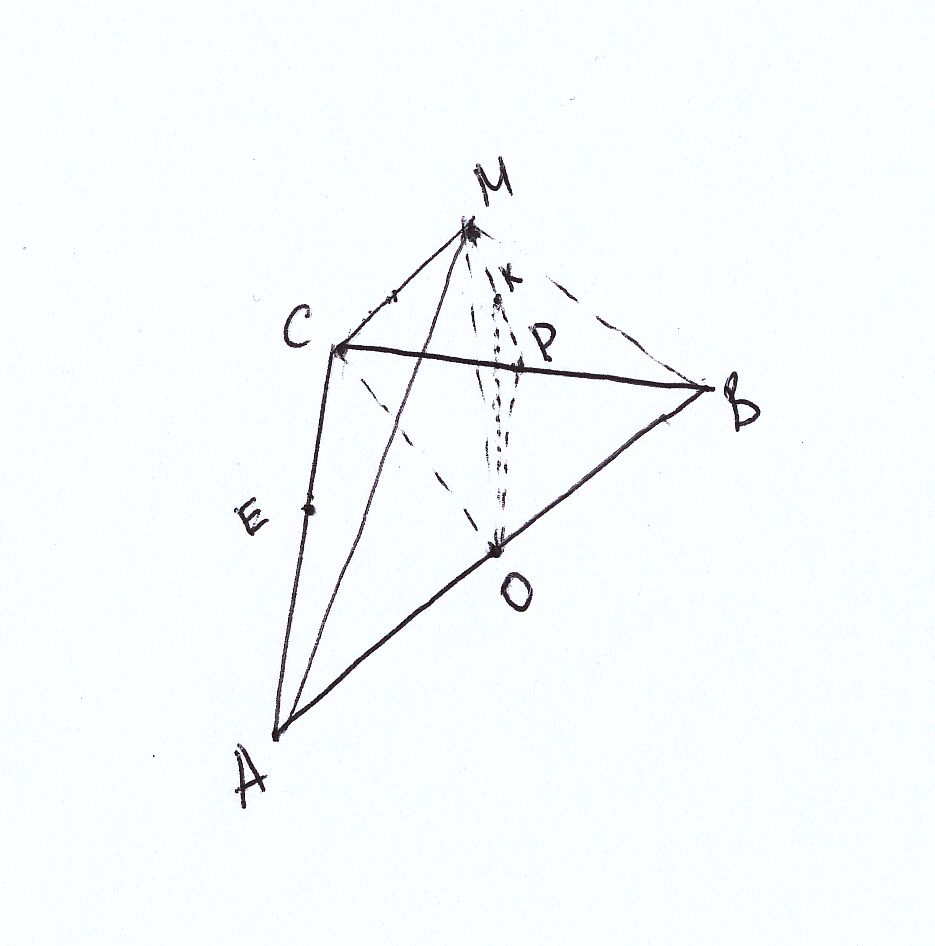