Диаметры оснований усеченного конуса равны 4 и 6. Найдите объем шара, вписанного в усеченный конус.

Решение: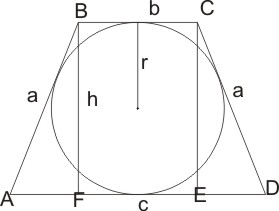

V=4/3 piR^3

 

Рассмотрим усеченный конус в продольном сечении. Это равнобедренная трапеция с основаниями AD=b=6 см и BC=a=4 см.

В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.: AB + DC = AD + BC или 2a = b + c

Бедро трапеции выражается через высоту по теореме Пифагора:

 BC = a = \√{h^{2}+(\frac{c-b}{2})^{2}

 

Зная, что 2a = b + c, получаем:

b+c=2\√{h^{2}+(\frac{c-b}{2})^{2}

Упростив выражение получим: h = \√{(\frac{c+b}{2})^{2}-(\frac{c-b}{2})^{2}

h = \frac{1}{2}\√{({c+b})^{2}-({c-b})^{2}

Используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим

h = \√{bc}

h = v(4*6) = v24 = 2v6

Радиус вписанной окружности равен половине высоты, т.к. центр окружности равноудален от точек касания со сторонами/основаниями трапеции.

r=?h=?*2v6=v6

 

Радиус рассмотренной окружности и будет радиусом шара

 

V = \frac{4}{3}piR^{3}  

V = \frac{4}{3}pi(\√{6})^{3}

V=\frac{4}{3}pi6\√{6}=8pi\√{6}

 

Ответ: V = 8pi√6