Основание пирамиды - равнобедренный треугольник с основанием а и углом при основании а. Все двугранные углы при основании пирамиды равны БЕТА.
а) докажите, что высота пирамиды проходит через центр окружности, вписанной в ее основание.
б) докажите, что проекции на плоскость основания высот боковых граней, проведенных из вершины пирамиды, равны, и найдите их длину.

Решение: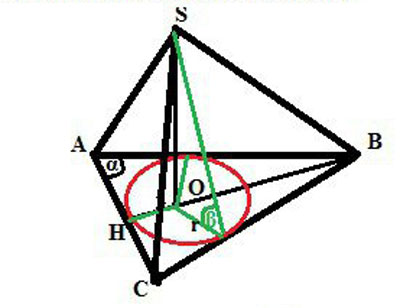

Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
Следовательно, двугранный угол при основании пирамиды равен линейному углу между высотой грани и ее проекцией на основание. Эта проекция - отрезок, соединяющий точку О, в которую проецируется высота пирамиды на основание пирамиды. Раз все двугранные углы равны, значит равны и эти отрезки и мы доказали пункт б).
Равенство этих проекций доказывает, что  точка О равноудалена от сторон треугольника. Это значит, что точка О - центр вписанной окружности в основание треугольника, то есть доказан пункт а).
Найдем длину проекции на плоскость основания высот боковых граней, проведенных из вершины пирамиды, или, как мы доказали, радиус вписанной в основание пирамиды окружности.
В равнобедренном треугольнике АВС BН - его высота, АН=НС=а/2.
Тогда АВ=АН/Cos? или AB=a/(2Cos?). BH=AB*Sin? или BH=a*Sin?/(2Cos?)=(а/2)*tg?.
Sabc=(1/2)*AC*BH или Sabc=(а/2)*(а/2)*tg?=(а?/4)*tg?.
Есть формула площади треугольника: S=p*r, где р - полупериметр,
r - радиус вписанной окружности. Тогда r=S/p или r=[(а?/4)*tg?]/p. p=2*AB+AC. Или
р=2*a/(2Cos?)+а=a/Cos?+а=а((1/Cos?)+1)=(а*(1+Cos?))/Cos?.
r=[(а?/4)*tg?]/[(а*(1+Cos?))/Cos?] или r=a*Sin?/[4(1+Cos?)].
Ответ: r=a*Sin?/[4(1+Cos?)].