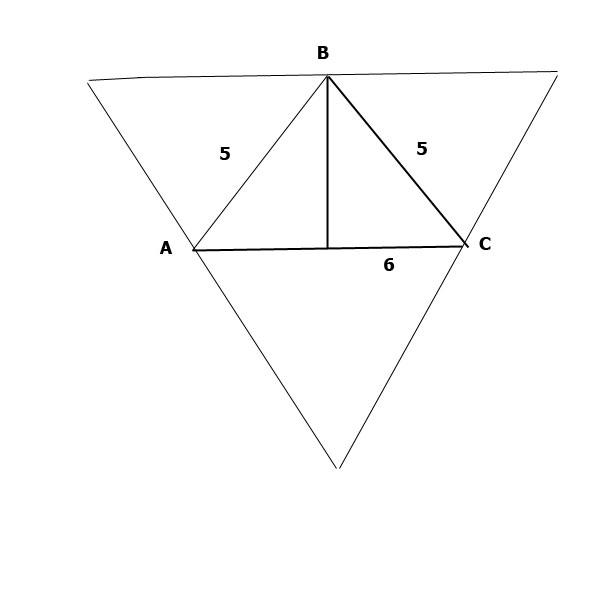
Основание АС равнобедренного треугольника АВС равно 6, а боковые стороны 5. Найдите расстояние между точками пересечения медиан и высот этого треугольника.

Решение:

Высота к основанию равна 4 (легко вычислить 5^2-(6/2)^2 = 4^2), она же и медиана, и обе точки лежат на ней.

Если достроить треугольник до "двойного" (через вершины треугольника провести линии, параллельные противоположным сторонам до пересечения), то медианы такого треугольника СОВПАДАЮТ с медианами исходного (вообще то это очевидно, но для вящей строгости скажем, что диагонали параллелограма делятся пополам в точках пресечения), медианы большого треугольника будут пересекать сторону исходного в середине, именно поэтому.

Точка же пересечения высот исходного треугольника для "двойного" является точкой пересечения медиатрисс (перпендикуляров из середин сторон), то есть это равноудаленная от вершин точка или центр описанной вокруг "двойного" треугольнка окружности.

Из простого чертежа ясно, что точка пересечения медиан отстоит от вершины исходного треугольника на расстояние (2/3)*m = 8/3;

Точка же пересечения медиатрисс "двойного" треугольника отстоит от основания "ДВОЙНОГО" треугольника (то есть от вершины исходного!) на расстояние

x = 2*m - R; где R - радиус описанной окружности ("двойного" треугольника!!!), ясно, что у вдвое меньшего исходного треугольника радиус описанной окружности тоже в 2 раза меньше.

Осталось вычислить R наиболее простым способом, например так

5/R = 8/10; Это записан косинус половины угла при вершине "двойного" треугольника.

R = 25/4, х = 7/4,

Ответ 8/3 - 7/4 = 11/12